SUMMARY
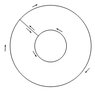
The discussion focuses on the parametrization of loops on a surface, specifically addressing the orientation of the first and last loops and the negative sign in the parametrization of the second loop, represented as (3cost; -3sint; 1/2). The right-hand rule is applied to determine the traversal direction of concentric circles, revealing that the outer circle is traversed clockwise while the inner circle must be traversed counterclockwise due to the normal vector's orientation. The negative sign in the second loop's parametrization indicates a reversal in direction, which is clarified through the transformation of the parameter t to -t.
PREREQUISITES
- Understanding of parametrization in multivariable calculus
- Familiarity with the right-hand rule in vector calculus
- Knowledge of normal vectors and their significance in surface orientation
- Basic comprehension of trigonometric functions and their graphical representations
NEXT STEPS
- Study the application of the right-hand rule in different geometric contexts
- Explore advanced topics in parametrization of surfaces in multivariable calculus
- Learn about the significance of normal vectors in surface integrals
- Investigate the effects of reversing parameters in parametric equations
USEFUL FOR
Students and professionals in mathematics, particularly those studying multivariable calculus, as well as educators seeking to clarify concepts related to surface parametrization and orientation.