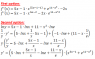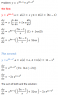- #1
BlaZz
- 3
- 0
Homework Statement
Image of the problem: http://prntscr.com/addkf
Homework Equations
My question is how I can solve the equation I gave above.
Should I use logarithmic differentiation?
Because I think that the logarithmic differentiation is used when y = (the equation) but my problem is f (x) = (the equation).
The Attempt at a Solution
Possible solutions: http://prntscr.com/addwu