Problem with length difference through circle

[MarkCJ]

Moved from non-homework section, so the homework template is missing.
Distance difference between A and B must be 0.25 or 0.75, find length of A and B in any possible value within radius of circle.

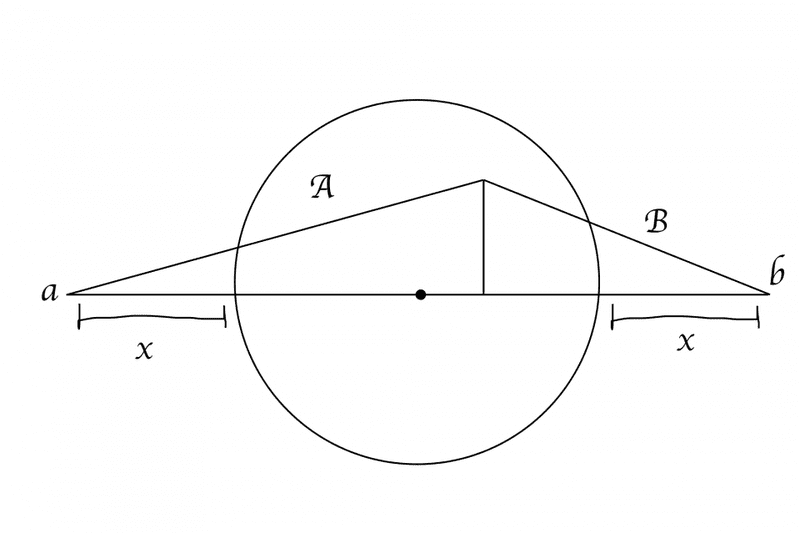
Is there a name of theory to find this problem?

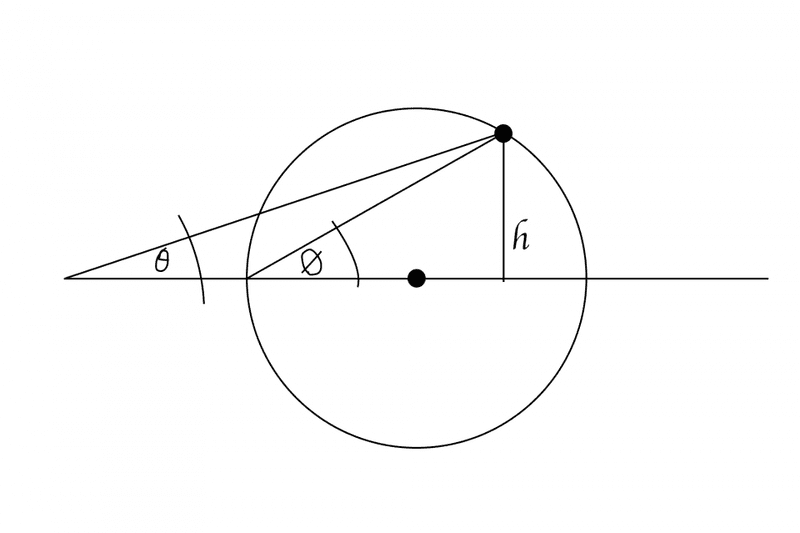
here's my try. for A at any point on circumference
A = { tan(ϑsinφ) [ r ( |sin(φ/2)| + 2|cos(φ)| )]} / sin(ϑsinφ)
ϑ = tan^-1r/(r+x) @ max height
φ = is radius of triangle in circle (circumference)
Obviously it is incorrect. :/

Thanks in advance for any answers or replies :-)

 

[Mark44]

Distance difference between A and B must be 0.25 or 0.75, find length of A and B in any possible value within radius of circle.
https://www.physicsforums.com/attachments/97044
Is there a name of theory to find this problem?

here's my try. for A at any point on circumference
A = { tan(ϑsinφ) [ r ( |sin(φ/2)| + 2|cos(φ)| )]} / sin(ϑsinφ)
ϑ = tan^-1(r/r+x) @ max height
φ = is radius of triangle in circle (circumference)

Thanks in advance for any answers or replies :-)

There are several confusing things here:
1. What does "|A - B| = 0.25, 0.75" mean?
2. That formula you have for A looks very complicated. Do you really mean tan(θsinφ) that you have in two places?
3. In your formula for θ, you have r/r + x. This means $\frac r r + x$. You probably meant $\frac r {r + x}$. If you don't use LaTeX, write this as r/(r + x).
4. What does "radius of triangle in circle (circumference)" mean?
5. Your drawing is pretty rough. Does the top vertex of the triangle lie on the circle?

 

[MarkCJ]

There are several confusing things here:
1. What does "|A - B| = 0.25, 0.75" mean?
2. That formula you have for A looks very complicated. Do you really mean tan(θsinφ) that you have in two places?
3. In your formula for θ, you have r/r + x. This means $\frac r r + x$. You probably meant $\frac r {r + x}$. If you don't use LaTeX, write this as r/(r + x).
4. What does "radius of triangle in circle (circumference)" mean?
5. Your drawing is pretty rough. Does the top vertex of the triangle lie on the circle?

Sorry, for my delay.
|A - B| = 0.25, 0.75 means distance difference between A and B must be 0.25 or 0.75. And, no, I didn't mean that, it was my try to make a formula for A at any circumference, x and r, to find |A-B|. φ = is radius of triangle in circle (circumference) or Φ. And, yes, I'm sorry I didn't make pictures clear enough but I changed it, I hope these are more obvious.

Thanks.

 

[Mark44]

Sorry, for my delay.
|A - B| = 0.25, 0.75 means distance difference between A and B must be 0.25 or 0.75.

The way to write that is $0.25 \le |A - B| \le 0.75$

And, no, I didn't mean that, it was my try to make a formula for A at any circumference, x and r, to find |A-B|.

φ = is radius of triangle in circle (circumference) or Φ.

You still didn't explain what "radius of triangle in circle (circumference)" means. From your revised drawing (the second one), I think you might mean the hypotenuse of the triangle that's inside the circle.

Your use of Greek letters is very confusing. In geometry and trig problems, Greek letters are typically used for angle measures, not length measures.

And, yes, I'm sorry I didn't make pictures clear enough but I changed it, I hope these are more obvious.

The pictures are much neater, but I'm still confused by a discrepancy between the first and second drawings. In the first, the vertical leg of both triangles doesn't extend all the way to the circle, but in the second drawing, it does.

Also, in the first drawing, the line through the center of the circle extends x units beyond the circle in either direction. I would use a different letter, since this distance is, I believe, constant. Instead, I would identify the piece of the horizontal line from the circle's center to the point where the vertical segment goes up to the circle.

I don't show the segments whose lengths are A and B. I am assuming that the center of the circle is at (0, 0).

Also, since this appears to be a homework problem, I am moving it to the Homework & Coursework section.

 

[RUber]

For this problem, I feel it is simpler to make your angle theta from the origin.
If you do that, then you can directly use $r\cos\theta$ as your variable distance x and $r\sin\theta$ as your variable height y.
I will use L to be the distance between the end points and the origin, i.e. a = (-L, 0), b = (L, 0).
Then you will end up with a relation between the hypotenuses:
$(r\sin\theta)^2 + (L - r\cos\theta)^2 = A\\ (r\sin\theta)^2 + (L + r\cos\theta)^2 = B$
Using the identity $\sin^2\theta = 1-\cos^2 \theta$, you can rewrite this problem to solve for $\cos^2\theta$.
Then you will get a solution in terms of r, which if you want to find a point inside the circle, you just use a smaller radius.

 

[MarkCJ]

I might inform this question incorrectly.
But let me try again.

The question is about finding any possible length of A and B that the difference between A and B is equal to 0.25 or 0.75
|A-B| = 0.25
|A-B| = 0.75
and the coordinates where line A and B meet must be within area of a circle of 0.5 radius.
It's later reveal that there're 12 possible points where this is possible.
from my guesses, there are 4 on (x,0), 2 on (x,y), 2 on (-x,y), 2 on (x,-y), and 2 on (-x,-y).
But the question is to find any possible value of A and B. or if there're more than 12 answers, is there a way to find it?

I will use L to be the distance between the end points and the origin, i.e. a = (-L, 0), b = (L, 0).

Given: L = 0.75, r = 0.5
Find A and B.

My question is how to find it?
I have tried to find a formula for every |A-B| at any r.

Also, since this appears to be a homework problem, I am moving it to the Homework & Coursework section.

Thanks, I'm new to this. :)

Again, thanks in advance.

 

[Mark44]

I might inform this question incorrectly.
But let me try again.

The question is about finding any possible length of A and B that the distance difference between A and B is equal to 0.25 or 0.75
|A-B| = 0.25
|A-B| = 0.75

You don't need to say "distance difference." Just plain difference is perfectly fine.
So |A - B| can only be those two values? Nothing in between?

and the coordinates where line A and B meet must be within area of a circle of 1 radius.
It's later reveal that there're 12 possible points where this is possible.
from my guesses, there are 4 on (x,0), 2 on (x,y), 2 on (-x,y), 2 on (x,-y), and 2 on (-x,-y).
But the question is to find any possible value of A and B. or if there're more than 12 answers, is there a way to find it?
Given: L = 0.75, r = 0.5
Find A and B.

Is the radius 1 or is it .5? A few lines up you say "a circle of 1 radius, but just above you say r = 0.5. Which is it?

My question is how to find it?
I have tried to find a formula for any |A-B| at any r.

OK, if I wasn't confused before, I really am, now. You have the radius of the circle being 1 in one place, 0.5 in another, and variable here.

I'm getting very frustrated with this problem. I've asked several questions in post #4 that you haven't answered. Please reread my post #4 and answer those questions.

 

[MarkCJ]

I think you might mean the hypotenuse of the triangle that's inside the circle.

Yes, my bad.

Your use of Greek letters is very confusing. In geometry and trig problems, Greek letters are typically used for angle measures, not length measures.

From ϑ = tan^-1(r/r+x) @ max height, yes that was badly explained.

Also, in the first drawing, the line through the center of the circle extends x units beyond the circle in either direction. I would use a different letter, since this distance is, I believe, constant.

Yes, it is constant. It was a roughly explained due to quick question. I imagine.

So |A - B| can only be those two values? Nothing in between?

No, nothing in between.

Is the radius 1 or is it .5? A few lines up you say "a circle of 1 radius, but just above you say r = 0.5. Which is it?
OK, if I wasn't confused before, I really am, now. You have the radius of the circle being 1 in one place, 0.5 in another, and variable here.

Haha, no, sorry for my typo. It's 0.5Sorry, for my bad English.

 

[Mark44]

Is the radius 1 or is it .5? A few lines up you say "a circle of 1 radius, but just above you say r = 0.5.
OK, if I wasn't confused before, I really am, now. You have the radius of the circle being 1 in one place, 0.5 in another, and variable here.

Haha, no, sorry for my typo.

But you didn't say what the radius is.
Is it 1, .5, or variable?

 

[MarkCJ]

But you didn't say what the radius is.
Is it 1, .5, or variable?

It's 0.5, but I also try to find the formula for this too.

 

[RUber]

I can't think of an easy formula for this.
As I mentioned earlier, you can define these relationships in terms of variables L, r, θ, and distance of separation d.
Again L is the distance from the origin, so a is at (-L, 0) and b is at (L, 0). r is the radius of the circle on which your point of intersection will lie. theta is the angle from the origin to the point of intersection, and d is the difference between the lengths of A and B.

Without loss of generality, let A be the longer leg.
This will be the first quadrant solution, and you can find the equivalent solutions in the remaining 3 quadrants easily.

|A-B|=d can be simplified as A-B=d.
Assuming that r < L.
$|A| = \sqrt{ (L+r\cos \theta)^2 + r^2 \sin^2 \theta} =\sqrt{L^2 + r^2 + 2Lr\cos\theta }\\ |B|= \sqrt{ (L-r\cos \theta)^2 + r^2 \sin^2 \theta}=\sqrt{L^2 + r^2 - 2Lr\cos\theta }$
Since subtracting radicals is tough, let's make this:
$(|A|-|B|)^2 =|A|^2 +|B|^2 -2|A||B| = d^2$
Which, after a fair amount of algebra, gives the answer.

 

[MarkCJ]

I can't think of an easy formula for this.

Thank you for your respond.
Yes, it's consider to be a somewhat hard question for me, I haven't try to find any solutions since my last post.

The hard part is to find A and B at any radius.

The question is about finding any possible length of A and B that the difference between A and B is equal to 0.25 or 0.75
|A-B| = 0.25
|A-B| = 0.75
and the coordinates where line A and B meet must be within area of a circle of 0.5 radius.
Given: L = 0.75, r = 0.5
Find A and B.

My question is how to find it?

Since r is variable compare to L is constant, for me this means I need special theory for this question or a 'trick'.
eg. |A-B| = 0.75, assume A > B then A => 0.75, then |A-B| = 0.75 can only occur at (x,0)

I can't think of an easy formula for this.

Can you think of any hard solutions for this? Please let me know.

Thanks :-)

 

[RUber]

When you say "within the area of a circle of radius 0.5," you are implying that if we define r as the distance from the origin to the point of intersection (P) where A and B meet, then $0\leq r\leq 0.5$, right?
Also, from your first post, you show L as the length extended past the radius of the circle. In my posts I was assuming that L was the length from the origin to points a or b.
In the method I was using, you would set d = 0.25 or d = 0.75 to find the solution to your specific problem.

Since r is variable compare to L is constant, for me this means I need special theory for this question or a 'trick'.
eg. |A-B| = 0.75, assume A > B then A => 0.75, then |A-B| = 0.75 can only occur at (x,0)

I am not sure I understand your logic.

The question is about finding any possible length of A and B that the difference between A and B is equal to 0.25 or 0.75
|A-B| = 0.25
|A-B| = 0.75
and the coordinates where line A and B meet must be within area of a circle of 0.5 radius.
It's later reveal that there're 12 possible points where this is possible.

This does not make sense based on your description of the problem.
You should have a continuous function of r on the interval $d/2 \leq r \leq 0.5$. This would imply there are infinitely many solutions.
At r = d/2, you would have solutions only at (d/2, 0) and (-d/2,0). But there is a first quadrant solution for every real r >d/2, and for every 1st quadrant solution, there are equivalent 2nd, 3rd, and 4th quadrant solutions.
Try working through the method I posted above. Find a few solutions by plugging in numbers and see if it makes sense.

If any of my assumptions are incorrect, please let me know.

 

[MarkCJ]

When you say "within the area of a circle of radius 0.5," you are implying that if we define r as the distance from the origin to the point of intersection (P) where A and B meet, then 0≤r≤0.50≤r≤0.50\leq r\leq 0.5, right?

Yes, I'd like to picture this problem in a infinite amount of circumference, eg. A on circumference ; at r = 0.45

Since r is variable compare to L is constant, for me this means I need special theory for this question or a 'trick'.
eg. |A-B| = 0.75, assume A > B then A => 0.75, then |A-B| = 0.75 can only occur at (x,0)

I am not sure I understand your logic.

Sorry, that was my bad I forgot to mention "if L = 0.5", I hope this makes it clear.

You should have a continuous function of r on the interval d/2≤r≤0.5d/2≤r≤0.5d/2 \leq r \leq 0.5. This would imply there are infinitely many solutions.

Yes, I also believe that there're infinite solutions, and this question do not explain why it has 12 possible points.
As I mentioned.

But the question is to find any possible value of A and B. or if there're more than 12 answers, is there a way to find it?

Many books claim that this is correct, and the question also ask to find how many points, which is really weird. I felt confused about literally everything, because I expected the answer to be infinite but instead it's 12 and it does not give coordinates of points. :/

If any of my assumptions are incorrect, please let me know.

Your assumptions are correct. Thank you for your replies. :)