Problem with one of the premises in electrostatic pressure theory

[physicsissohard]

TL;DR

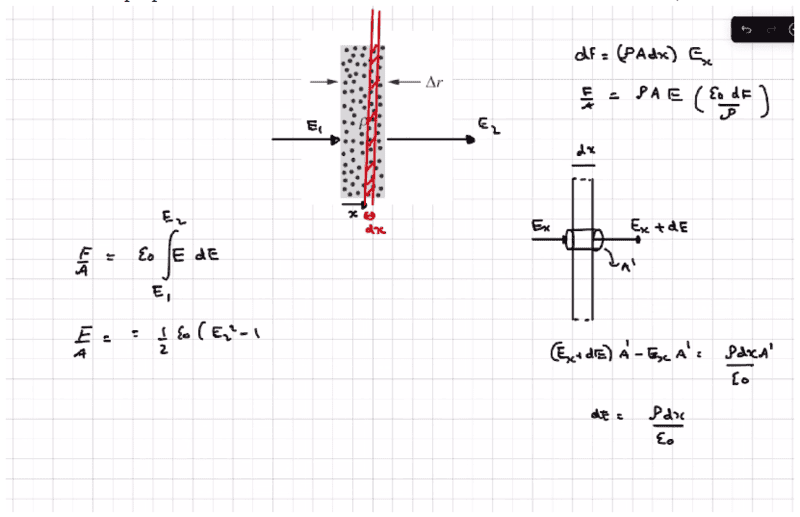
I was watching a video and he was trying to derive a result in electrostatic pressure. He was deriving the pressure on a differential area element of a hollow conducting sphere. He did it two ways, the second way was straightforward he did it by using only gauss's law and a neat argument but the first derivation I have a problem.

I have the video linked with the time stamp. . Isn't Electric Field anywhere inside the conductor zero. So there will be no electric field inside the thickness of the conductor. But he managed to integrate it somehow? he considered electric field to be changing inside the conductor that has density rho and did it. But proprties of conductors state that elctric field inside conductor is zero, doesn't it?

 

[TSny]

Isn't Electric Field anywhere inside the conductor zero. So there will be no electric field inside the thickness of the conductor. But he managed to integrate it somehow? he considered electric field to be changing inside the conductor that has density rho and did it. But proprties of conductors state that elctric field inside conductor is zero, doesn't it?

The charge at the surface of a conductor in electrostatic equilibrium is not actually in a layer of zero thickness. The surface charge is nonzero within a very thin layer at the surface. There is a nonzero volume charge density and a nonzero electric field within this layer. As you pass through this layer from just outside the conductor, the electric field changes continuously from its value just outside the surface to zero. The electric field is zero everywhere inside the conducting material except for points within this layer.

In many situations, we treat the layer as having zero thickness and model the electric field as having a jump discontinuity at the surface. However, the video shows how to derive the force per unit area on the surface charge of the conductor by treating the layer as having finite thickness. This derivation follows that of Purcell's textbook.