- #1
trenekas
- 61
- 0
I have a problem. Here is the task. Need to prove all these claims:
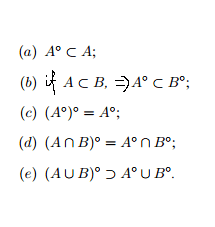
I was able to prove only one and half of them.
b) Let A[itex]\subset[/itex]B and x [itex]\in[/itex] A°. It mean that there is ε>0 that Oε(x)[itex]\subset[/itex]A. And it mean that Oε(x)[itex]\subset[/itex]A[itex]\subset[/itex]B. And that mean that x[itex]\in[/itex]B, what I need to prove.
c) (A°)°[itex]\subset[/itex]A° it follows from a. if i could prove that :D
How to prove A°[itex]\subset[/itex] (A°)° i don't know. tried to apply definition but nothing goes on.
Can you give me some advise which way i need to go?
I was able to prove only one and half of them.
b) Let A[itex]\subset[/itex]B and x [itex]\in[/itex] A°. It mean that there is ε>0 that Oε(x)[itex]\subset[/itex]A. And it mean that Oε(x)[itex]\subset[/itex]A[itex]\subset[/itex]B. And that mean that x[itex]\in[/itex]B, what I need to prove.
c) (A°)°[itex]\subset[/itex]A° it follows from a. if i could prove that :D
How to prove A°[itex]\subset[/itex] (A°)° i don't know. tried to apply definition but nothing goes on.
Can you give me some advise which way i need to go?
Last edited:
 ))
))