bearn
- 11
- 0
What are the step-by-step in solving these problems?
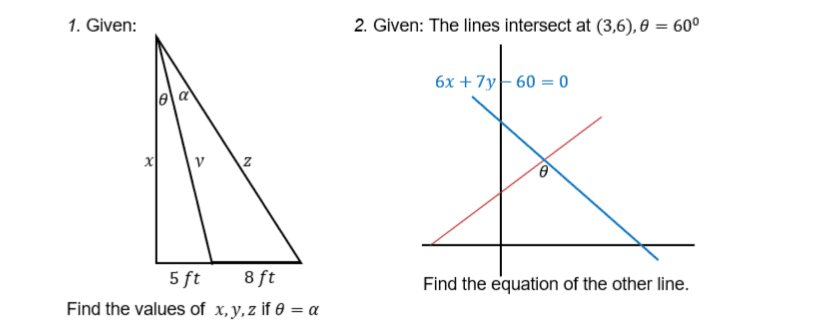
This discussion focuses on solving problems involving trigonometric identities, specifically using the tangent function and angle relationships in right triangles. The first problem utilizes the identity for tangent of double angles, tan(2θ) = 2tan(θ)/(1 - tan²(θ)), to derive equations for x based on given values. The second problem involves calculating angles and slopes from a linear equation, 6x + 7y = 60, leading to the determination of the slope of a red line as tan(79.4) = 5.34. The discussion emphasizes the importance of understanding right triangle properties and trigonometric identities in problem-solving.
PREREQUISITESStudents and educators in mathematics, particularly those focusing on trigonometry, geometry, and algebra. This discussion is beneficial for anyone looking to enhance their problem-solving skills in trigonometric contexts.
Country Boy said:For (1) I assume the lower left angle is a right angle.
Got it! Thank You so much!Country Boy said:For (2) the blue line is given by 6x+ 7y= 60 or y= -(6/7)x+ 60/7. Its slope is -6/7 so the "exterior angle" of that triangle is arctan(-6/7)= 139.4 degrees. The interior angle is 180- 139.4= 40.6 degrees. Since $\theta= 60$ degrees the third angle, where the red line crosses the base is 180- 60- 40.6= 120- 40.6= 79.4 degrees. So the slope of the red line is tan(79.4)= 5.34.
y= 5.34(x- x_0)+ y_0 where (x_0, y_0) is any point on the line. We are told that (3, 6) is such a point.