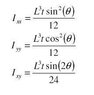Product moment of inertia of an inclined section of a beam

In summary, the conversation revolves around deriving the Ixy equation using simple integration and the difficulty in calculating the first moment of area on an inclined section. The conversation also touches on the use of cosine and sine functions, and the limits for the integral.
  • #1
emRage
5
0
Hi guys,

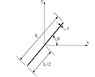
I would like to derive the Ixy equation from simple integration and I can't seem to get the right answer (third equation down the picture). I seem to be able to derive Ixx and Iyy easily but product moment of area requires first moment of area to be calculated and I just don't know how to do that on an inclined section.

Any help would be apprecited on this issue.

Thank you.
 

Attachments

  • un.JPG
    un.JPG
    9 KB · Views: 3,739
  • un1.JPG
    un1.JPG
    5.7 KB · Views: 3,338
Engineering news on Phys.org
  • #2
Welcome to PF!

Hi emRage! Welcome to PF! :wink:

Is the rod in the x-y plane? And what is t?

ok, you need to prove that Ixy = L3t(sin2θ)/24.

Show us the integral you have for this. :smile:​
 
  • #3
This one I've figured out! :-p

x = cos(theta) . s
y = sin(theta) . s
dA = ds . thickness
limits for s = L/2 and -L/2

Thanks anyway!
 

1. What is the product moment of inertia of an inclined section of a beam?

The product moment of inertia of an inclined section of a beam is a measure of its resistance to bending. It takes into account both the shape and orientation of the section, and is used to calculate the deflection and stress in the beam.

2. How is the product moment of inertia of an inclined section of a beam calculated?

The product moment of inertia of an inclined section of a beam is calculated by multiplying the moment of inertia of the section about its neutral axis by the cosine squared of the angle between the neutral axis and the inclined section.

3. What factors affect the product moment of inertia of an inclined section of a beam?

The product moment of inertia of an inclined section of a beam is affected by the shape and dimensions of the section, as well as the angle of inclination. The material properties of the beam also play a role in determining its product moment of inertia.

4. Why is the product moment of inertia important in structural analysis?

The product moment of inertia is a crucial parameter in structural analysis because it determines the bending stiffness of a beam. This affects the deflection and stress in the beam, which are important considerations in designing safe and efficient structures.

5. How does the product moment of inertia differ from the moment of inertia?

The product moment of inertia is a modified version of the moment of inertia that takes into account the orientation of the section. While the moment of inertia is a scalar quantity, the product moment of inertia is a vector quantity that varies in different directions. The two are related by the cosine of the angle between the neutral axis and the inclined section.

Similar threads

Moment of inertia question for two plates welded together
    • Mechanical Engineering
Replies
11
Views
1K
What would be the ideal cross section of an axially loaded cantilever beam?
    • Mechanical Engineering
Replies
2
Views
1K
What is the best beam design for my aluminum tandem axle trailer?
    • Mechanical Engineering
Replies
33
Views
3K
Understanding the Value of the Second Moment Of Area
    • Mechanical Engineering
Replies
7
Views
2K
Box Beam stress problem with welding
    • Mechanical Engineering
Replies
16
Views
1K
How to add area moments of inertia for varying cross sections
    • Mechanical Engineering
Replies
4
Views
4K
Can You Subtract Moments of Inertia to Find the MOI of Unknown Sections?
    • Mechanical Engineering
Replies
1
Views
994
Calculate the residual stress on a beam after bending
    • Mechanical Engineering
Replies
30
Views
4K
Second moment of inertia for a bent rectangle
    • Mechanical Engineering
Replies
7
Views
2K
Calculating shear in a cantelever
    • Mechanical Engineering
Replies
1
Views
962

Hot Threads

Recent Insights

Back
Top