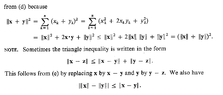Proof of Apostol's Definition 3.2 and Theorem 3.3: Help Appreciated

[Math Amateur]

I am reading Tom M Apostol's book "Mathematical Analysis" (Second Edition) ...I am focuses on Chapter 3: Elements of Point Set Topology ... I need help regarding a remark of Apostol's made after Definition 3.2 and Theorem 3.3 ...Definition 3.2 and Theorem 3.3 read as follows:
View attachment 8477
View attachment 8478
In a note at the end of the proof of parts of Theorem 3.3 we read the following:

"... ... We also have

$$\mid \ \parallel x \parallel - \parallel y \parallel \ \mid \ \leq \ \parallel x - y \parallel$$ ... Could someone please show me how top formally and rigorously prove that ...$$\mid \ \parallel x \parallel - \parallel y \parallel \ \mid \ \leq \ \parallel x - y \parallel$$ ...

Help will be appreciated ...

Peter

 

[GJA]

Hi Peter,

Could someone please show me how top formally and rigorously prove that ...
$$\mid \ \parallel x \parallel - \parallel y \parallel \ \mid \ \leq \ \parallel x - y \parallel$$ ...

Here are a few hints:

1. Write $\|x\| = \|x-y +y\|.$
2. Use the triangle inequality.
3. Obtain a lower bound for $\|x-y\|$.
4. Repeat the above with $\|y\|,$ obtaining a lower bound for $\|y-x\| = \|x-y\|.$
5. Note that the two lower bounds differ by a negative sign only.
6. Conclude that ${\large |}\|x\| - \|y\|{\large|}\leq \|x-y\|$ since $${\large |}\|x\|-\|y\|{\large |}=\begin{cases}\|x\|-\|y\| & \|x\|\geq \|y\|\\ \|y\| - \|x\| & \|y\|\geq \|x\|. \end{cases}$$

Let me know if anything is still unclear.

 

[S.G. Janssens]

You are right to ask this question. It is called the "reverse triangle inequality". You can try to prove it yourself by using the ordinary triangle inequality to estimate both $\|x\| = \|(x - y) + y\|$ and $\|y\| = \|(y - x) + x\|$.

EDIT: Sorry, I did not see the reply by GJA and the system did not warn me when I submitted mine.

 

[Math Amateur]

Hi Peter,
Here are a few hints:

1. Write $\|x\| = \|x-y +y\|.$
2. Use the triangle inequality.
3. Obtain a lower bound for $\|x-y\|$.
4. Repeat the above with $\|y\|,$ obtaining a lower bound for $\|y-x\| = \|x-y\|.$
5. Note that the two lower bounds differ by a negative sign only.
6. Conclude that ${\large |}\|x\| - \|y\|{\large|}\leq \|x-y\|$ since $${\large |}\|x\|-\|y\|{\large |}=\begin{cases}\|x\|-\|y\| & \|x\|\geq \|y\|\\ \|y\| - \|x\| & \|y\|\geq \|x\|. \end{cases}$$

Let me know if anything is still unclear.

Thanks GJA ...

Working through your post ...

Appreciate your help...

Peter

 

[Math Amateur]

You are right to ask this question. It is called the "reverse triangle inequality". You can try to prove it yourself by using the ordinary triangle inequality to estimate both $\|x\| = \|(x - y) + y\|$ and $\|y\| = \|(y - x) + x\|$.

EDIT: Sorry, I did not see the reply by GJA and the system did not warn me when I submitted mine.

Thanks for the guidance and help, Janssens

Peter