Proof of T.a=0 rule in mechanics (Laws of motion)

[Rinzler09]

There is this T.a rule in laws of motion which can be applied to a system to solve problems regarding constraint motion. Here's an example

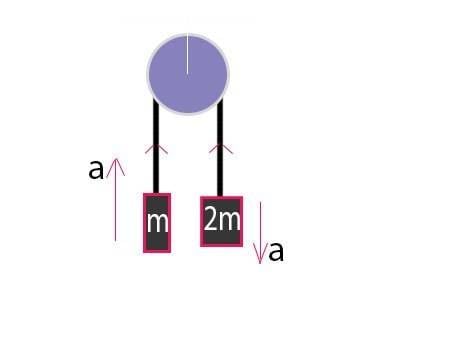
This example is pretty simple so I've decided to show the application of the rule here.
Consider the FBD of m,
T is in the same direction as the acceleration. Therefore, T.a=Ta₁
Considering the FBD of 2m,
T is in the opposite direction. Therefore, T.a=-Ta₂

ΣT.a=0, Therefore, Ta₁ - Ta₂=0
Thus, a₁=a₂

This method is really useful for complex pulley systems such as this one.

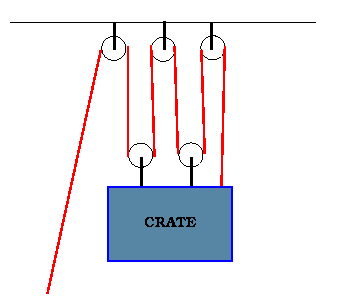
I was wondering how to prove this. Can somebody help? Just give me an idea. Don't post the proof.

 

[BvU]

Well hello Rinzler, welcome to PF !

If you consider the constant length of the rope, it is pretty straightforward that y₁ + y₂ is a constant.
So v₁ + v₂ = 0 and a₁ + a₂ = 0 too.

The pulley system you draw is somewhat different, though

 

[Rinzler09]

Well hello Rinzler, welcome to PF !

If you consider the constant length of the rope, it is pretty straightforward that y₁ + y₂ is a constant.
So v₁ + v₂ = 0 and a₁ + a₂ = 0 too.

The pulley system you draw is somewhat different, though

Yeah, the length of the string is constant. But I'm saying that ΣT.a for the system is zero.

 

[BvU]

Doesn't feel good to me: the dimension of $\vec T \cdot \vec a$ is all irregular.
$\sum \vec T \cdot \vec a = 0$ only because $\sum \vec a = \vec 0$ and the T are equal.

Newton $\sum \vec F = m\vec a$ would be a lot better starting point for your analysis of e.g. the crate system.
And (with due care for the masses of the pulleys -- they can be different, equal, massless or all on one and the same axle) there will be an additional statement for the tensions.

 

[nasu]

A single object accelerating under the action of a single tension (like a block pulled on a horizontal surface) does not satisfy this "rule".
As for the system in OP, why not sum of accelerations or sum of tensions? They are also zero but so what? It's not a general relationship.