Constraint Forces and Lagrange Multipliers

[deuteron]

TL;DR Summary

why are the gradients of the holonomic constraints perpendicular to the constraint forces

My question is about the general relationship between the constraint functions and the constraint forces, but I found it easier to explain my problem over the example of a double pendulum:
Consider a double pendulum with the generalized coordinates $q=\{l_1,\theta_1,l_2,\theta_2\}$,:

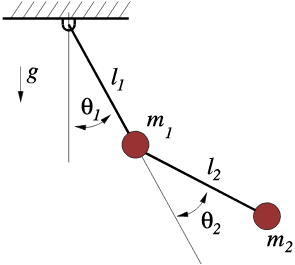
The set of constraint functions is:
$$f=\begin{pmatrix} l_1-\text{const.}_1\\ l_2-\text{const.}_2\end{pmatrix}=0$$

Since $f=0$ describes the level curve $N_0(f)$, it describes a submanifold in the configuration space, the generalized coordinates of phase space
Since this is a level curve, $\nabla f$ is perpendicular to the manifold embedded in the configuration space
However, the constraint *forces* act on the physical plane of motion, which is a submanifold in $3d$ space
Therefore, I don't understand how we can say that $\nabla f\| F_\text{constraint}$ in the Lagrangian mechanics, since they act on manifolds embedded in different spaces

 

[vanhees71]

Let's write it down for a general case of one particle subject to one constraint, i.e., a particle moving on some surface. Then the Lagrangian reads
$$L=\frac{m}{2} \dot{\vec{x}}^2 - V(\vec{x})$$
and the (holonomous) constraint
$$f(\vec{x})=0.$$
The constraint can be implemented using the Lagrange-multiplier method, i.e., you add to the variation of the action $-\lambda \delta \vec{x} \cdot \vec{\nabla} f$. This leads to the Euler-Lagrange equations,
$$m \ddot{\vec{x}}=-\vec{\nabla} V-\lambda \vec{\nabla} f.$$
The 2nd term on the right-hand side are the "constraint forces". Since also the constraint itself must be fulfilled you have
$$0=\frac{\mathrm{d}}{\mathrm{d} t} f(\vec{x})=\dot{\vec{x}} \cdot \vec{\nabla} f=0,$$
and thus with
$$\vec{F}_{\text{constraint}}=-\lambda \vec{\nabla} f \; \Rightarrow \; \dot{\vec{x}} \cdot \vec{F}_{\text{constraint}}=0,$$
i.e., the contraint forces are prependicular to the tangent vectors $\dot{\vec{x}}$ on the surface, described by the constraint.

The same holds of course in terms of any other coordinates as in your example. Only there of course you have two constraints constraining the mass points from the original 4D space to a 2D submanifold.