Proof of Wheatstone bridge equation

[whatdoido]

Homework Statement

Prove the following equation:

$\Delta U=\frac {R_1R_4}{(R_1+R_4)^2}(\frac {\Delta R_1}{R_1}-\frac {\Delta R_2}{R_2}+\frac{\Delta R_3}{R_3}-\frac{\Delta R_4}{R_4})E$

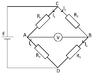
This is used in Wheatstone bridge

Homework Equations

[/B]
U=RI

The Attempt at a Solution

This has been a real head-scratcher

Two voltage dividers can be found for starters. Voltage's direction is assumed to be clockwise

$V_{in1}=I_2(R_2+R_3)$

$I_2=\frac{V_{in1}}{R_2+R_3}$

$V_{out1}=I_2R_3$

$V_{out1}=V_{in1}\frac{R_3}{R_2+R_3}$

Similarly:

$V_{out2}=V_{in1}\frac{R_4}{R_1+R_4}$

$V_G$ is voltage between A and B

$V_{out1}-V_{out2}=V_G$

$V_{in1}\frac{R_3}{R_2+R_3}-V_{in1}\frac{R_4}{R_1+R_4}=V_G$

$V_{in1}(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})=V_G$

$V_{in1}=E$

$V_G=\Delta U$ so then

$E(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})=\Delta U$

I have calculated voltages in different circuits and tried to think this problem in different ways, but the real problem is that how is $\Delta R_i$ inserted into equations. Assumption goes that it is added by $R_i+\Delta R_i$. Maybe that is incorrect?

Help is very much appreciated!

edit: Misspelling corrected

Also particularizing that $\Delta R_i$ is a change in one resistance

 

[haruspex]

that $\Delta R_i$ is a change in one resistance

Which suggests that the Δ in ΔU refers to the consequent change in U, not to the potential difference between A and B at a given set of R values.

 

[whatdoido]

Which suggests that the Δ in ΔU refers to the consequent change in U, not to the potential difference between A and B at a given set of R values.

Yes that is true, $\Delta U$ is zero before the change of resistances.

 

[haruspex]

Yes that is true, $\Delta U$ is zero before the change of resistances.

So this equation:
$E(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})=\Delta U$
Should read
$E(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})=U$
and you need a different expression for $\Delta U$.

 

[whatdoido]

Right now I'm trying to figure out why this would not be possible:

$E(\frac{R_3+\Delta R_3}{R_2+\Delta R_2+R_3+\Delta R_3}-\frac{R_4+\Delta R_4}{R_1+\Delta R_1+R_4+\Delta R_4})=\Delta U$

I can simplify it a bit, but is this the right way to go

 

[haruspex]

Right now I'm trying to figure out why this would not be possible:

$E(\frac{R_3+\Delta R_3}{R_2+\Delta R_2+R_3+\Delta R_3}-\frac{R_4+\Delta R_4}{R_1+\Delta R_1+R_4+\Delta R_4})=\Delta U$

I can simplify it a bit, but is this the right way to go

I do not see how you get that. It looks wrong.
You have an equation for U (second eqn in post #4). Write out the corresponding eqn for U+ΔU.

 

[whatdoido]

I do not see how you get that. It looks wrong.
You have an equation for U (second eqn in post #4). Write out the corresponding eqn for U+ΔU.

Now that I thought about it, simply adding the change does not make so much sense.

But then I got an idea to take partial derivates since it is about change. Adding those partial derivates together should give the overall change in voltage.

$U=E(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})$

Seems like marking $U$ as $U_{BA}$ is needed since I took potential difference with $V_{out1}-V_{out2}=V_G$

$U_{BA}=(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})E$

This should be legal: $\Delta U_{BA}=dU_{BA}$

Thus $dU_{BA}=\frac {\partial} {\partial R_1}U_{BA}\Delta R_1+\frac {\partial} {\partial R_2}U_{BA}\Delta R_2+\frac {\partial} {\partial R_3}U_{BA}\Delta R_3+\frac {\partial} {\partial R_4}U_{BA}\Delta R_4$

Solving partial derivates each:

$\frac {\partial} {\partial R_1}U_{BA}\Delta R_1=\frac {\partial} {\partial R_1}(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})E\Delta R_1=-\frac {R_4}{(R_1+R_4)^2}E\Delta R_1$

$\frac {\partial} {\partial R_2}U_{BA}\Delta R_2=\frac {\partial} {\partial R_2}(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})E\Delta R_2=\frac{R_3}{(R_2+R_3)^2}E\Delta R_2$

$\frac {\partial} {\partial R_3}U_{BA}\Delta R_3=\frac {\partial} {\partial R_3}(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})E\Delta R_3=-\frac{R_2}{(R_2+R_3)^2}E\Delta R_3$

$\frac {\partial} {\partial R_4}U_{BA}\Delta R_4=\frac {\partial} {\partial R_4}(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})E\Delta R_4=\frac{R_1}{(R_1+R_4)^2}E\Delta R_4$

$dU_{BA}=-\frac {R_4}{(R_1+R_4)^2}E\Delta R_1+\frac{R_3}{(R_2+R_3)^2}E\Delta R_2-\frac{R_2}{(R_2+R_3)^2}E\Delta R_3+\frac{R_1}{(R_1+R_4)^2}E\Delta R_4$

$dU_{BA}=(-\frac{R_4}{R_1(1+\frac{R_4}{R_1})^2}\frac{\Delta R_1}{R_1}+\frac{R_3}{R_2(1+\frac{R_4}{R_1})^2}\frac{\Delta R_2}{R_2}-\frac{R_2}{R_3(1+\frac{R_1}{R_4})^2}\frac{\Delta R_3}{R_3}+\frac{R_1}{R_4(1+\frac{R_1}{R_4})^2}\frac{\Delta R_4}{R_4})E$

I just kept playing with the identity $\frac{R_2}{R_3}=\frac{R_1}{R_4}$ and I got:

$dU_{BA}=\frac{R_1R_4}{(R_1+R_4)^2}(-\frac{\Delta R_1}{R_1}+\frac{\Delta R_2}{R_2}-\frac{\Delta R_3}{R_3}+\frac{\Delta R_4}{R_4})E$

It has wrong signs because of $V_{out1}-V_{out2}=V_G$

So I think the equation is about $U_{AB}$

$\Delta U_{AB}=dU_{AB}=-dU_{BA}=-\frac{R_1R_4}{(R_1+R_4)^2}(-\frac{\Delta R_1}{R_1}+\frac{\Delta R_2}{R_2}-\frac{\Delta R_3}{R_3}+\frac{\Delta R_4}{R_4})E$

$=\frac{R_1R_4}{(R_1+R_4)^2}(\frac{\Delta R_1}{R_1}-\frac{\Delta R_2}{R_2}+\frac{\Delta R_3}{R_3}-\frac{\Delta R_4}{R_4})E$

 

[haruspex]

Looks good.