- #1
control
- 14
- 0
Homework Statement
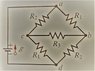
Set voltage between 1. a-b; 2- b-c; 3 c-d 4. a-c; if voltage of battery is 12V and R_1=2000 ohms R_2=3000 ohms; R_3= 4000 ohms. (see attached file)
Homework Equations
voltage=final voltage- innitial voltage
resistors in series R_1,2=R_1+R_2
parallel resistors: R_1,2=(R_1*R_2)/(R_1+R_2)
The Attempt at a Solution
I have no idea how to solve such problem. I can use Kirchhoff laws in circuits, I can use all equations I wrote in "relevant equations", I watched video how to set equivalent resistance of those resistors through "delta to ypsilon transformation" () but I have absolutely no idea how to apply my knowledge in such problem.
Attachments
Last edited by a moderator: