So the shortest title I can come up with is: Complex Numbers and Real Solutions

[Dank2]

I haven't learn using e yet, is it possible to do it with r(cosx+isinx) ?

 

[Sahil Kukreja]

I haven't learn using e yet, is it possible to do it with r(cosx+isinx) ?

In other questions e can be useful, but in this question you can use both the ways and get the answer in same time( actually same efficiency)

 

[Ray Vickson]

I have solved it

It is a violation of PF rules for you to post this. You are not supposed to present solutions!

 

[Dank2]

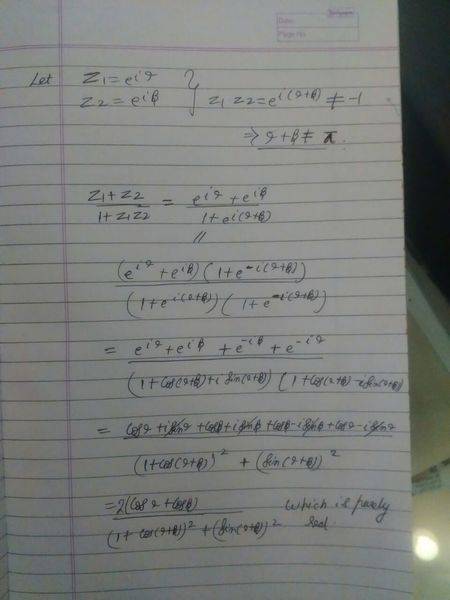
I haven't learn using e yet, is it possible to do it with r(cosx+isinx) ?[/QUOT

In other questions e can be useful, but in this question you can use both the ways and get the answer in same time( actually same efficiency)

Work to do, therefore ! It's almost more efficient to teach you this $e^{i\phi}$ than to drudge through all this cos sin and such...
But I can be hired to do your work if you pay better than my boss ... .

it's just 4 terms that needs to be organized, cause we don't matter about the real part

 

[Sahil Kukreja]

It is a violation of PF rules for you to post this. You are not supposed to present solutions!

Sorry. I have deleted the solution now

 

[Sahil Kukreja]

I have another method to solve and it is a lot easier:- (it just solves in three steps)

Hint:-
z' --> conjugate of z
if z-z' = 0 then z is purely real

also use that since |z1|=|z2|=1
then z1=1/z1' and z2=1/z2'

 

[Sahil Kukreja]

Now, I have a third method to solve :-
since |z1|=|z2|=1
then z1=1/z1' and z2=1/z2'

put this in the equation and use your previous knowledge to get the answer

 

[Dank2]

I have another method to solve and it is a lot easier:- (it just solves in three steps)

Hint:-
z' --> conjugate of z
if z-z' = 0 then z is purely real

also use that since |z1|=|z2|=1
then z1=1/z1' and z2=1/z2'

Very nice! it came so smooth, thank you sir, and also, for all the others that helped . i didn't even use z1 =1/z1'.

 

[Sahil Kukreja]

Very nice! it came so smooth, thank you sir, and also, for all the others that helped . i didn't even use z1 =1/z1'.

its good to remember that z.z' = $|z|^2$

 

[Dank2]

its good to remember that z.z' = $|z|^2$

yes i followed that, and all the terms in the numerator left was z1-z1' + z2-z2' which is ofc real, and denominator was 1+z1z2 + conjugate(z1z2), which is also real.

 

[BvU]

Very nice! it came so smooth, thank you sir, and also, for all the others that helped . i didn't even use z1 =1/z1'.

I learned from this too : even though you have found a way through (and I thought the $e^{i\phi}$ was pretty efficient ) , it's good to keep an eye open for alternatives, and Sahil had no trouble pointing out a very good one !

 

[Sahil Kukreja]

yes i followed that, and all the terms in the numerator left was z1-z1' + z2-z2' which is ofc real, and denominator was 1+z1z2 + conjugate(z1z2), which is also real.

z1-z1' + z2-z2' is not purely real, its purely imaginary.
z=(z1+z2)/(1+z1z2)
if you put z1=1/z1' and z2=1/z2' then you must have gotten z=z'
which implies z is purely real.

 

[Dank2]

z1-z1' + z2-z2' is not purely real, its purely imaginary.
z=(z1+z2)/(1+z1z2)
if you put z1=1/z1' and z2=1/z2' then you must have gotten z=z'
which implies z is purely real.

Ok , now i know that i had to use that z1=1/z1'

so it came up 1/z'+1/z+1/z2+1/z2', and i forgot to add |z1z2|^2 at the denominator in message #45