Prove the sums of the angles of any given triangle = 180°

[r0bHadz]

Homework Statement

Prove that if A,B,C, are the angles of an arbitrary triangle, then

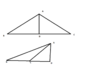
m(A)+m(B)+m(C) = 180 degrees by the following method: From any vertex draw the perpendicular to the line of the opposite side. Then use the result already known for right triangles

Homework Equations

The Attempt at a Solution

I think I can break this proof down into 3 cases

a right triangle, with base b and height h, with the perpendicular of the vertex

a triangle with height h, and a base b+x, x>0 where its perpendicular is x units to the left of the right triangles perpendicular

a triangle with height h, and a base b+k k<0 where its perpendicular is k units to the left of the right triangles perpendicular

am I right here or are there other cases i need to consider?

 

[YoungPhysicist]

To me,a simpler version will be:

Any triangle can be copied and flipped and placed beside the original one and form a rectangle,square, or parallelogram.

All of the three shapes above has the inner angle sum of 360 degrees, so $\frac{360}{2} = 180$.

 

[r0bHadz]

To me,a simpler version will be:

Any triangle can be copied and flipped and placed beside the original one and form a rectangle,square, or parallelogram.

All of the three shapes above has the inner angle sum of 360 degrees, so $\frac{360}{2} = 180$.

This is my method as well but I am trying to follow the prompt given

 

[r0bHadz]

I might just skip this because it's worded pretty weirdly tbh.. i don't even know if I get what it means. and like Yung physicist said, there is much easier way to prove what he is asking

 

[TachyonLord]

Homework Statement

Then use the result already known for right triangles

Which results are you implying here ?

 

[r0bHadz]

Which results are you implying here ?

If you have a right triangle, two angles will add up to 90 degrees

 

[Delta2]

You basically have to consider these two cases where the height of the triangle ABC from vertex A, to side BC, the height being AD, and D is either inside BC or it meets the extension of the side BC.

In both cases you consider the right triangles ABD, ACD (D the right angle) and right two equations using the known result for right triangles. You add the two equations (or subtract the two equations in the second case with D outside) and you prove what is needed to be proved.

Oh and there is the third case where the triangle ABC is right, this case follows directly from the known result that you have to use.

EDIT : The case with D outside needs a bit more special treatment but the general idea remains the same.

 

[r0bHadz]

You basically have to consider these two cases where the height of the triangle ABC from vertex A, to side BC, the height being AD, and D is either inside BC or it meets the extension of the side BC.

In both cases you consider the right triangles ABD, ACD (D the right angle) and right two equations using the known result for right triangles. You add the two equations (or subtract the two equations in the second case with D outside) and you prove what is needed to be proved.View attachment 236391

Oh and there is the third case where the triangle ABC is right, this case follows directly from the known result that you have to use.

EDIT : The case with D outside needs a bit more special treatment but the general idea remains the same.

Hmm. So for the first one, since I already know a right triangle has an angle of 90 degrees, and the sum of the remaining two angles = 90deg, that leave A1+C = 90, and A2+B= 90, adding together A1+A2+B+C=190, but A1+A2= A so A+B+C=180 deg

For the second one,

lets say C1 and A1 are inside the right triangle

we have C1+A1+90=180
C1+A1=90C1+C2=180
C1 = 180-C2

180-C2+A1= 90

A1+A2+B= 90

(90-C1)+A2+B=90

(90-(180-C2))+A2+B=90

-90 + C2 + A2 + B = 90

C2+A2+B = 180

 

[Delta2]

I think you are right (as long as C1,C2, A1,A2 are the angles I think they are). Forgot to mark all the proper angles in the schemes.

 

[TachyonLord]

If you have a right triangle, two angles will add up to 90 degrees

But that does arise from the angle sum property right ? So we're assuming that its true for right triangles and then proving for others ? (acute and obtuse triangles ?)

 

[SammyS]

But that does arise from the angle sum property right ? So we're assuming that its true for right triangles and then proving for others ? (acute and obtuse triangles ?)

@r0bHadz does not state how the case for a right triangle was presented. However, the instructions state to use that result.

If you follow the sequence of posts referencing this issue, this becomes reasonably clear.

Homework Statement

Prove that if A,B,C, are the angles of an arbitrary triangle, then

m(A)+m(B)+m(C) = 180 degrees by the following method: From any vertex draw the perpendicular to the line of the opposite side. Then use the result already known for right triangles.

Which results are you implying here ?

If you have a right triangle, two angles will add up to 90 degrees

I assume that @r0bHadz means 'the two acute angles add to 90 °.' .

 

[Svein]

Hint:

α+β+γ=360°
∠CBA = ½β (why?)
etc.

 

[neilparker62]

Homework Statement

Prove that if A,B,C, are the angles of an arbitrary triangle, then

m(A)+m(B)+m(C) = 180 degrees by the following method: From any vertex draw the perpendicular to the line of the opposite side. Then use the result already known for right triangles

Referring to the top diagram in post 7, I assume the "result already known" means $D_1=D_2=90$ (degrees). Then : $$D_2=B+A_1 $$ and $$D_1=C+A_2 $$ with D₁ and A₁ being in the left hand triangle. I'm not quite sure if we are "allowed" to invoke the theory regarding external angle of triangle as I have done ? In the second diagram (post 7) , we should perhaps rather drop the perpendicular from vertex C.