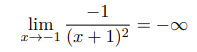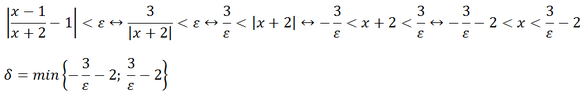SUMMARY
This discussion focuses on proving limits at infinity using the formal definition of limits. The first limit, $$\lim_{x\to\infty}\frac{x-1}{x+2} = 1$$, requires demonstrating that for any $$\varepsilon > 0$$, there exists an $$N$$ such that $$\left|\frac{x-1}{x+2} - 1\right| < \varepsilon$$ for $$x > N$$. The second limit, $$\lim_{x\to-1}\frac{-1}{(x+1)^2} = -\infty$$, involves showing that for any $$M$$, a $$\delta > 0$$ can be found such that $$\frac{-1}{(x+1)^2} < -M$$ whenever $$|x+1| < \delta$$. The discussion emphasizes the importance of manipulating inequalities to find suitable values for $$N$$ and $$\delta$$.
PREREQUISITES
- Understanding of limits in calculus
- Familiarity with the epsilon-delta definition of limits
- Basic algebraic manipulation skills
- Knowledge of approaching infinity in mathematical contexts
NEXT STEPS
- Study the epsilon-delta definition of limits in depth
- Practice proving limits at infinity with various functions
- Explore the concept of limits approaching negative infinity
- Learn about asymptotic behavior of functions
USEFUL FOR
Students in calculus, mathematics educators, and anyone seeking to strengthen their understanding of limits and their proofs in mathematical analysis.