Proving limit of rational function

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

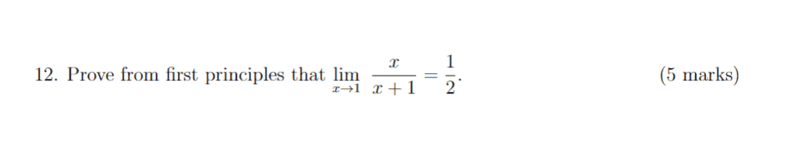
The solution is,

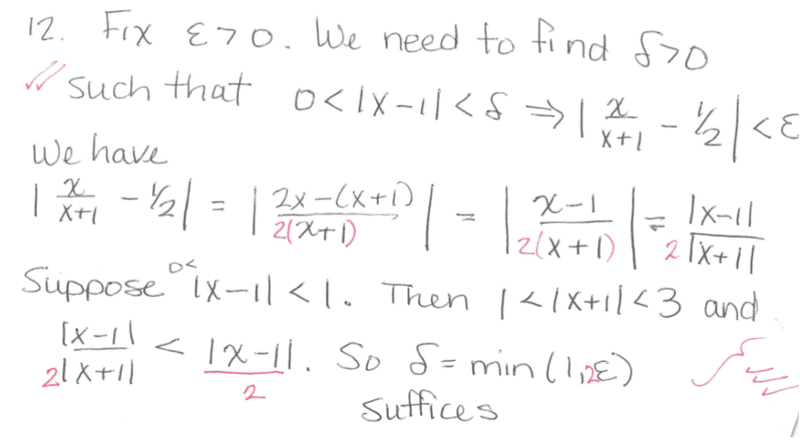
However, I'm confused how $0 < | x - 1|< 1$ (Putting a bound on $| x- 1|$) implies that $1 < |x+1| < 3$. Does someone please know how?

My proof is,
$0 < | x - 1|< 1$
$|2| < | x - 1| + |2| < |2| + 1$
$2 < |x - 1| + |2| < 3$
Then take absolute values of all three sides of the equation,
$|2| < ||x - 1| + |2|| < |3|$
This allows us to remove the absolute values around the x - 1 and 2. Thus,
$|2| < |x - 1 + 2| < |3|$
$|2| < |x + 1| < |3|$
$2 < |x + 1| < 3$

However, the two on the LHS side is wrong.

Thanks!

 

[anuttarasammyak]

\frac{x}{x+1}=1-\frac{1}{x+1}
The problem is reduced to prove
\lim_{x \rightarrow 1} \frac{1}{x+1} = \frac{1}{2} or further
\lim_{x \rightarrow 1} x = 1

 

[member 731016]

\frac{x}{x+1}=1-\frac{1}{x+1}
The problem is reduced to prove
\lim_{x \rightarrow 1} \frac{1}{x+1} = \frac{1}{2} or further
\lim_{x \rightarrow 1} x = 1

Thank you for your reply @anuttarasammyak! That is actually a very interesting idea to prove a rational function converges from first principles by decomposing the rational function by using partial fractions then using algebra of limits. I think you could also use first principles on $x$ and $x + 1$ by using the definition of limit, then maybe add the results? I.e prove that x goes to 1 as x goes to 1, and x + 1 goes to 2 as x goes to 1 respectively? However, how would we add these epsilon and delta proof to prove that our rational function converges to $\frac{1}{2}$. Do you please know whether we just divide them, by each other or something like that?

However, do you please know how to solve using my method?

Thanks!

 

[fresh_42]

We are interested in the neighborhood of $x=1$ so assuming $0< |x-1|<1$ is not a problem. The left inequality is always true, and the right one means
\begin{align*}
|x-1| < 1 \Longleftrightarrow 0<x<2 \Longleftrightarrow 1<x+1<3
\end{align*}
We get therefore
$$
\dfrac{|x-1|}{2|x+1|} < \dfrac{1}{2|x+1|} < \dfrac{1}{2\cdot 1}=\dfrac{1}{2}
$$
But this isn't small enough. We have to narrow down $|x-1|$. If $\delta = 2\varepsilon$ and $|x-1| < \delta$ then
$$
\dfrac{|x-1|}{2|x+1|} < \dfrac{\delta}{2|x+1|}=\dfrac{2\varepsilon }{2|x+1|} < \dfrac{2\varepsilon }{2\cdot 1}=\varepsilon .
$$

 

[member 731016]

We are interested in the neighborhood of $x=1$ so assuming $0< |x-1|<1$ is not a problem. The left inequality is always true, and the right one means
\begin{align*}
|x-1| < 1 \Longleftrightarrow 0<x<2 \Longleftrightarrow 1<x+1<3
\end{align*}
We get therefore
$$
\dfrac{|x-1|}{2|x+1|} < \dfrac{1}{2|x+1|} < \dfrac{1}{2\cdot 1}=\dfrac{1}{2}
$$
But this isn't small enough. We have to narrow down $|x-1|$. If $\delta = 2\varepsilon$ and $|x-1| < \delta$ then
$$
\dfrac{|x-1|}{2|x+1|} < \dfrac{\delta}{2|x+1|}=\dfrac{2\varepsilon }{2|x+1|} < \dfrac{2\varepsilon }{2\cdot 1}=\varepsilon .
$$

Thank you for your reply @fresh_42!

That is very helpful. However, do you please know why my proof for the absolute value implication is wrong?

Thanks!

 

[fresh_42]

Thank you for your reply @fresh_42!

That is very helpful. However, do you please know why my proof for the absolute value implication is wrong?

Thanks!

What do you mean? The picture you uploaded was ok, except for the corrected factor $2.$

Do you mean what you typed below your picture? I guess ...

This allows us to remove the absolute values around the x - 1 and 2.

... is the culprit, but I am notoriously bad with absolute values. I always have to scribble a lot to get it right.

My solution was $0<|x-1|<1 \Longrightarrow 0<x<2 \Longrightarrow 1<x+1<3.$ I don't understand why you made it so complicated.

 

[anuttarasammyak]

However, do you please know how to solve using my method?

d:= x-1
|\frac{x}{1+x}-\frac{1}{2}|=\frac{1}{4}|\frac{d}{1+\frac{d}{2}}| &lt; |d|
for $d$ satisfying
-1 &lt; d &lt; 1
[EDIT] I had confused the two and corrected. By contgrolling $d$ we can make it smaller than any given constant.

 

[fresh_42]

Say
\epsilon = x-1
|\delta|=|\frac{x}{1+x}-\frac{1}{2}|=\frac{1}{4}|\frac{\epsilon}{1+\frac{\epsilon}{2}}| &lt; |\epsilon|
for $\epsilon$ satisfying
-1 &lt; \epsilon &lt; 1

This is nothing but confusing.

 

[FactChecker]

However, I'm confused how $0 < | x - 1|< 1$ (Putting a bound on $| x- 1|$) implies that $1 < |x+1| < 3$. Does someone please know how?

Since $|x-1| < 1, 0 < x < 2$. Therefore, $1<x+1< 3$.

$|2| < ||x - 1| + |2|| < |3|$
This allows us to remove the absolute values around the x - 1 and 2. Thus,
$|2| < |x - 1 + 2| < |3|$

This is wrong. If $x-1 < 0$ then $x-1+2 <2$. It is possible that $|x-1+2| < 2$.

However, do you please know how to solve using my method?

I think it may be fundamentally flawed.

 

[Orodruin]

It should be pointed out why the assumption $|x-1| < 1$ is made here: The purpose is to find a $\delta$ such that $x/(x+1)$ differs from 1/2 by at most $\epsilon$. Restricting $\delta < 1$ is not a problem - if you could find a $\delta \geq 1$, a $\delta < 1$ would clearly also suffice.

The issue if you do not restrict $\delta$ to some value smaller than 2, then $x+1 = 0$ becomes a possibility and $|x/(x+1)|$ is unbounded. Particularly larger than $\epsilon$ around $x = -1$. So we choose to restrict $\delta$ to avoid this. Then, as mentioned above, we need to further restrict $\delta$ for values of $\epsilon > 1/2$.

Note that we could have chosen $\delta < k < 2$ instead. This would imply
$$
\frac{|x-1|}{|x+1|} < \frac{k}{2-k}
$$
which is sufficient if $\epsilon > k/(2(2-k))$. If not, then
$$
\frac{|x-1|}{|x+1|} < \frac{\delta}{2-k}
$$
and choosing $\delta < (2-k)2\epsilon$ works.