pitaly
- 6
- 1
- TL;DR
- Proof of theorem. Intuition: local maxima and global maxima coincide for concave functions
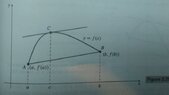
Consider the following theorem:
Theorem: Let ##f## be a concave differentiable function and let ##g## be a concave function. Then: ##y \in argmax_{x} {f(x)+g(x)}## if and only if ##y \in argmax_{x} {f(y)+f'(y)(x-y)+g(x)}.##
The intuition is that local maxima and global maxima coincide for concave functions. But can anyone help me with a formal proof? Thanks in advance!
Theorem: Let ##f## be a concave differentiable function and let ##g## be a concave function. Then: ##y \in argmax_{x} {f(x)+g(x)}## if and only if ##y \in argmax_{x} {f(y)+f'(y)(x-y)+g(x)}.##
The intuition is that local maxima and global maxima coincide for concave functions. But can anyone help me with a formal proof? Thanks in advance!