Pulley Acceleration and Tension Relations

[inv4lid]

Homework Statement

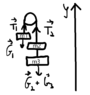
Determine bodies' acceleration if their masses are the following: m1 = 25kg, m2 = 1kg, m3 = 3kg and the Tension of the ropes. Friction is neglected, as well as the mass of the pulley. It is considered that the ropes are perfect.

m₁ = 25kg;
m₂=1kg;
m₃=3kg;
___________
a=?
T₁=?
T₂=?
#

Homework Equations

For the first object we have:
T₁-G₁= m1*a; (the acceleration is oriented upwards)
a = (T₁-G₁)/m₁;
For next ones, I guess:
The acceleration here goes downwards
T₂-G₂-G₃ = -(m₂+m₃)*a;
a = (T₂-G₂ - G₃) / -(m₂ + m₃)

Are the accelerations the same?
How would i find it?

 

[kuruman]

Are the accelerations the same?

What would happen if the accelerations were not the same?
You may safely assume that this is an ideal pulley, i.e. it changes the direction of the tension but not its magnitude. This will simplify your work.

 

[inv4lid]

What would happen if the accelerations were not the same?
You may safely assume that this is an ideal pulley, i.e. it changes the direction of the tension but not its magnitude. This will simplify your work.

I need to get some numbers. How would i get the tension/acceleration? There is too much unknown data.
(i guess we can't get any of T)

 

[NFuller]

I need to get some numbers. How would i get the tension/acceleration? There is too much unknown data.
(i guess we can't get any of T)

I think kuruman is trying to get you to relate $T_{1}$ to $T_{2}$. If the pulley is ideal (frictionless and massless) what is the relation? Once you have the relation, you can solve the algebraic system.