Adesh
- 735
- 191
- Homework Statement
- Find the equations of path difference and the equations for maxima and minima.
- Relevant Equations
- #path~difference ~= d\sin\theta#.
If I put a slab of some material whose refractive index is \mu and width is D, in front of slits in Young's Double Slit model, then
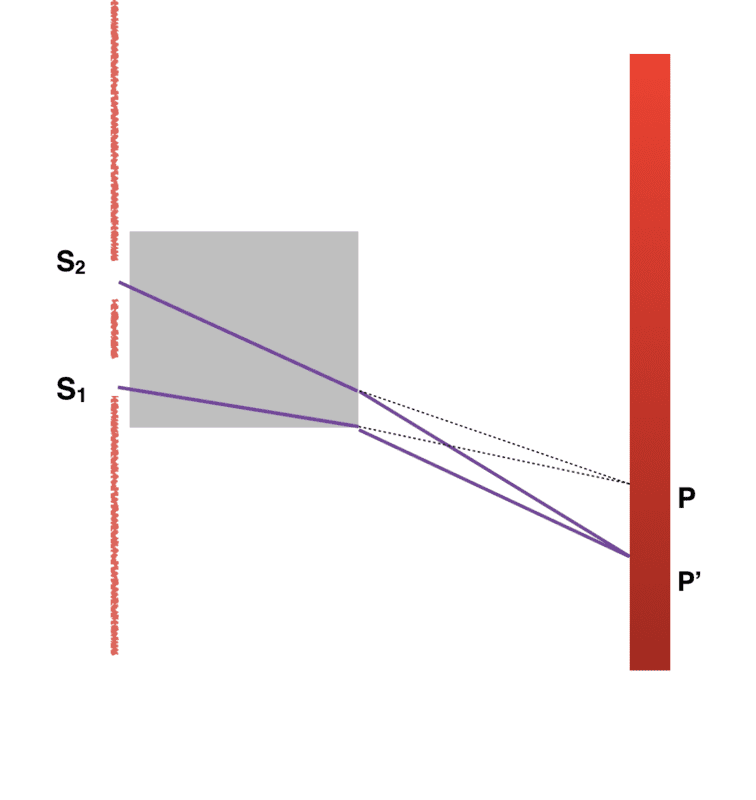
In the figure you can see that I have placed the slab just after the slits. So, when rays going to come out of the slab they will bend away from normal (here I'm assuming that the material of the slab is optically denser than the air) and due to this bend they will intersect at P' and if the slab were to be absent they would have met at P. So, a pattern at P has shifted to P' but what is the itexematics of it? How to derive equations for path difference in this situation? Do we draw a perpendicular from S_1 to S_2P like usual, but S_2P is not a single line it gets bent just after the slab. How should I begin?
In the figure you can see that I have placed the slab just after the slits. So, when rays going to come out of the slab they will bend away from normal (here I'm assuming that the material of the slab is optically denser than the air) and due to this bend they will intersect at P' and if the slab were to be absent they would have met at P. So, a pattern at P has shifted to P' but what is the itexematics of it? How to derive equations for path difference in this situation? Do we draw a perpendicular from S_1 to S_2P like usual, but S_2P is not a single line it gets bent just after the slab. How should I begin?