Homework Help Overview
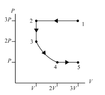
The discussion revolves around a problem involving a pV diagram and the ranking of heat transfer during four thermodynamic processes. Participants are exploring concepts related to the first law of thermodynamics, work done by gases, and the ideal gas law.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation
Approaches and Questions Raised
- Participants are attempting to calculate changes in thermal energy (ΔEth), work done by the gas (Wgas), and the absolute value of heat transfer (|Q|) for each process. There are questions about the meaning of absolute values in this context and the reasoning behind specific calculations, particularly for process 3->4.
Discussion Status
Some participants have provided guidance on using the ideal gas law and integrating to find work, while others express constraints against using integrals. There is an ongoing exploration of how to approach the calculations without integrals, and some participants are updating their understanding based on feedback.
Contextual Notes
Participants are working under specific homework constraints that limit the methods they can use, such as avoiding integrals. There is also a noted confusion regarding the representation of zero values in the context of thermal energy changes.