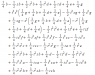benpaulthurston
- 5
- 0
I found this formula for doing a quadratic conformal map with parameters:
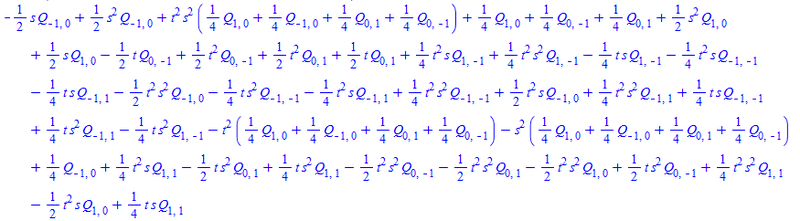
I think there's probably a nice Einstein notation representation of this above but I haven't figured it out yet.. But anyway the mapping is like below:
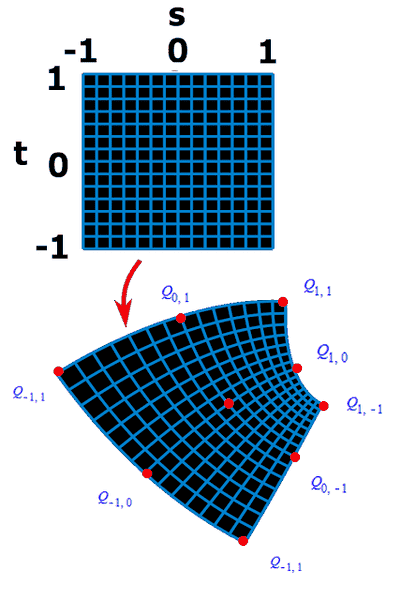
I don't know enough about General Relativity to know how this would fit in exactly, but so far I've written a program in Python to do this with images:

Any comments are appreciated, thanks!
I think there's probably a nice Einstein notation representation of this above but I haven't figured it out yet.. But anyway the mapping is like below:
I don't know enough about General Relativity to know how this would fit in exactly, but so far I've written a program in Python to do this with images:
Any comments are appreciated, thanks!