eprparadox
- 133
- 2
I'm watching a lecture on the intro to quantum computing.
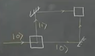
See the attached image which will be useful as I describe my question.
So the professor says that we have this single photon and it's in this state, ## | 0 > ##.
He states that when we send this photon through a beam splitter that it will (assuming we're not doing any sort of measurement), end up in a superposition state of
\frac{1}{\sqrt{2}}( |0> + |1>)
If you look at beam splitter 1 (BS1) in the image, you'll see the incoming photon in state ## |0> ## and two outgoing states, ## |0> ## to the right and ## |1>## up.
My question is this: considering this superposition state, does it even make sense to think about these two different paths? Or is EACH outgoing path through BS1 this same superposition state of
\frac{1}{\sqrt{2}}( |0> + |1>)
Put another way, should I basically think about the beamsplitter as this black box that takes an input and just outputs a single superposition state into the next beam splitter?
Thanks a lot.
See the attached image which will be useful as I describe my question.
So the professor says that we have this single photon and it's in this state, ## | 0 > ##.
He states that when we send this photon through a beam splitter that it will (assuming we're not doing any sort of measurement), end up in a superposition state of
\frac{1}{\sqrt{2}}( |0> + |1>)
If you look at beam splitter 1 (BS1) in the image, you'll see the incoming photon in state ## |0> ## and two outgoing states, ## |0> ## to the right and ## |1>## up.
My question is this: considering this superposition state, does it even make sense to think about these two different paths? Or is EACH outgoing path through BS1 this same superposition state of
\frac{1}{\sqrt{2}}( |0> + |1>)
Put another way, should I basically think about the beamsplitter as this black box that takes an input and just outputs a single superposition state into the next beam splitter?
Thanks a lot.