Question about a partial derivative

[George Keeling]

TL;DR Summary

Problem with partial derivative when one variable depends on the other.

I apologise for the length of this question. It is probably possible to answer it by reading the first few lines. I fear I have made a childish error:

I am working on the geodesic equation for the surface of a sphere. While doing so I come across the partial derivative
\begin{align}
\frac{\partial}{\partial\theta}\left(\sin^2{\phi}\right)=0?&\phantom {10000}(1)\nonumber
\end{align}where $\phi, \theta$ are colatitude(angle from north pole) and longitude. I could say that the expression must vanish because $\phi,\theta$ are orthogonal. But I know thate $\phi$ is a function $\theta$ so I could say, using the chain rule twice, that the expression is\begin{align}
\frac{\partial}{\partial\theta}\left(\sin^2{\phi}\right)=2\sin{\phi}\cos{\phi}\frac{d\phi}{d\theta}?&\phantom {10000}(2)\nonumber
\end{align}The answer might be very obvious and simple. I think the former is correct but would like some confirmation please.

The detailed reasons for the question are given below. They include my fears about the metric.

The geodesic equation is
\begin{align}
\frac{d^2x^\sigma}{d\lambda^2}+\Gamma_{\mu\nu}^\sigma\frac{dx^\mu}{d\lambda}\frac{dx^\nu}{d\lambda}=0&\phantom {10000}(3)\nonumber
\end{align}where $\Gamma$ is the Christoffel symbol (torsion-free and metric compatible), given by
\begin{align}
\Gamma_{\mu\nu}^\sigma=\frac{1}{2}g^{\sigma\rho}\left(\partial_\mu g_{\nu\rho}+\partial_\nu g_{\rho\mu}-\partial_\rho g_{\mu\nu}\right)&\phantom {10000}(4)\nonumber
\end{align}The coordinates are $x^0=\phi$ and $\ x^1=\theta$ and the metric and inverse metric are
\begin{align}
g_{\mu\nu}=\left(\begin{matrix}1&0\\0&\sin^2{\phi}\\\end{matrix}\right)\ \ ,\ \ g^{\mu\nu}=\left(\begin{matrix}1&0\\0&\sin^{-2}{\phi}\\\end{matrix}\right)&\phantom {10000}(5)\nonumber
\end{align}$\lambda$ will parameterise a line which gives the required geodesic. First I derived what these equations mean and I get two second order differential equations involving $\phi,\theta,\lambda$. I believe these are
\begin{align}
\frac{d^2\phi}{d\lambda^2}-\sin{\phi}\cos{\phi}\left(\frac{d\theta}{d\lambda}\right)^2=0&\phantom {10000}(6)\nonumber
\end{align}and
\begin{align}
\frac{d^2\theta}{d\lambda^2}+2\cot{\phi}\frac{d\phi}{d\lambda}\frac{d\theta}{d\lambda}=0&\phantom {10000}(7)\nonumber
\end{align}There were two ways to work these equations out. Assuming (2) (that ${\partial f(\phi)}/{\partial\theta}\neq0$) each method gave a different answer for equation (7) unless I made a mistake, which is quite likely.

I have not yet tried to solve these equations, but I know that a geodesic on a sphere is a great circle so I can work out its equation and it can be written
\begin{align}
\theta=\lambda\ \ ,\ \ \phi=\tan^{-1}{\left(\frac{C}{A\cos{\lambda}+B\sin{\lambda}}\right)}&\phantom {10000}(8)\nonumber
\end{align}where $A,B,C$ are constants depending on the start and end points (in quite a complicated way.) It should be simple to check that (8) satisfies (6) and (7). Clearly $\phi$ depends only on $\theta$ and the start and end points, as one would expect. This leads to the original question.

I checked my equation (8) by using my wonderful 3-D plotter. The geodesics look perfect.

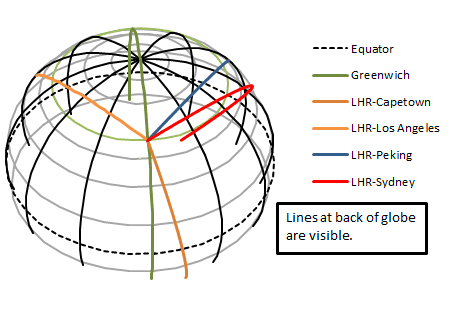
I also searched the internet for the equation and found one on Wolfram MathWorld (http://www.mathworld.wolfram.com/GreatCircle.html). It was slightly different from mine and cause me great pain. It is incorrect! Their colatitudes and latitudes are mixed up. I have told them, but there is no response. I also plotted their solution and it gave a rather long route to Peking. Whatever the case $\phi$ depends on $\theta$ and the start and end points.

(8) tells us that
\begin{align}
\frac{d^2\theta}{d\lambda^2}=0&\phantom {10000}(9)\nonumber
\end{align}Which does not sit well with (7). If I had the metric at (5) 'the wrong way round', it would be
\begin{align}
g_{\mu\nu}=\left(\begin{matrix}\sin^2{\phi}&0\\0&1\\\end{matrix}\right)\ \ ,\ \ g^{\mu\nu}=\left(\begin{matrix}\sin^{-2}{\phi}&0\\0&1\\\end{matrix}\right)&\phantom {10000}(10)\nonumber

\end{align}this would have given (9) at (7). However I want to cross one bridge at a time …

 

[Mark44]

Summary: Problem with partial derivative when one variable depends on the other.

I am working on the geodesic equation for the surface of a sphere. While doing so I come across the partial derivative
\begin{align}
\frac{\partial}{\partial\theta}\left(\sin^2{\phi}\right)=0?&\phantom {10000}(1)\nonumber
\end{align}where $\phi, \theta$ are colatitude(angle from north pole) and longitude. I could say that the expression must vanish because $\phi,\theta$ are orthogonal. But I know thate $\phi$ is a function $\theta$ so I could say, using the chain rule twice, that the expression is\begin{align}
\frac{\partial}{\partial\theta}\left(\sin^2{\phi}\right)=2\sin{\phi}\cos{\phi}\frac{d\phi}{d\theta}?&\phantom {10000}(2)\nonumber
\end{align}The answer might be very obvious and simple. I think the former is correct but would like some confirmation please.

It seems to me that $\phi$ and $\theta$ are independent, meaning that $\phi$ is not a function of $\theta$. As you said, $\phi$ is the angle measured from the north pole (z-axis), and $\theta$ is the angle measured from what would be the x-axis in the x-y plane. The two coordinates are independent, so $\partial \left(\frac{ \sin^2(\phi)}{\partial \theta}\right) = 0$.

 

[George Keeling]

Thanks, but then there's my equation (8) which effectively says that$$
\phi=\tan^{-1}{\left(\frac{C}{A\cos{\theta}+B\sin{\theta}}\right)}
$$ so it might seem that $\phi$ does depend on $\theta$. This is my quandary.

 

[Mark44]

Thanks, but then there's my equation (8) which effectively says that$$
\phi=\tan^{-1}{\left(\frac{C}{A\cos{\theta}+B\sin{\theta}}\right)}
$$ so it might seem that $\phi$ does depend on $\theta$. This is my quandary.

But this isn't consistent with your descriptions of what $\phi$ and $\theta$ represent. If they truly are spherical coordinates, they are unrelated to each other.

 

[fresh_42]

Equations $(8)$ look like a parameterization of a certain path, not a general dependence.

 

[George Keeling]

Equations (8) look like a parameterization of a certain path, not a general dependence.

Indeed it is the equation of a curve, light dawns! Thanks, I can get on.

 

[haushofer]

Maybe unnecessary, but students have similar confusion when you give them a path in classical mechanics,

$$x(t)$$

with a certain speed $\frac{dx(t)}{dt}$, and then the remark that spacetime is spanned by space and time coordinatens, and hence

$$\partial_t x = 0$$

Of course, this last equation holds for general coordinates; but as soon as you introduce a path $x(t)$ in space(time), you introduce for that path a certain relation between the coordinates $t$ and $x$.

 

[Orodruin]

Maybe unnecessary, but students have similar confusion when you give them a path in classical mechanics,

$$x(t)$$

with a certain speed $\frac{dx(t)}{dt}$, and then the remark that spacetime is spanned by space and time coordinatens, and hence

$$\partial_t x = 0$$

Of course, this last equation holds for general coordinates; but as soon as you introduce a path $x(t)$ in space(time), you introduce for that path a certain relation between the coordinates $t$ and $x$.

... and let's not get into field theory where you have to teach students to tell apart partial derivatives with respect to the space-time variables from partial derivatives of the Lagrangian - especially when the Lagrangian has an explicit dependence on the space-time variables ...