SUMMARY
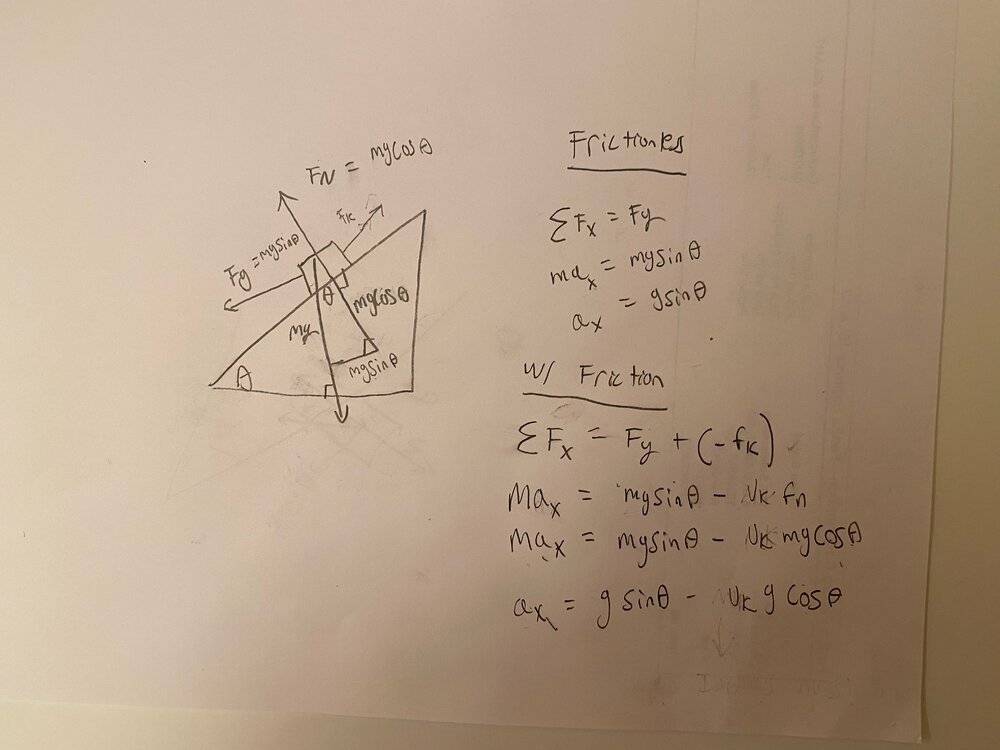
The discussion centers on the physics of inclined planes, specifically addressing how mass affects acceleration and friction. It is established that while mass does not influence acceleration on an inclined plane, increased weight on a sled enhances speed due to reduced friction from snow compaction and melting. The conversation also highlights the role of air resistance and its dependency on surface area, particularly in sledding and bobsledding contexts, where teams may add ballast to meet weight requirements for optimal performance.
PREREQUISITES
- Understanding of Newton's laws of motion
- Basic principles of friction and its coefficients
- Knowledge of air resistance and its effects on moving objects
- Familiarity with bobsledding rules and weight regulations
NEXT STEPS
- Research the physics of inclined planes and acceleration
- Explore the effects of snow compaction on sledding dynamics
- Learn about air resistance and its calculation in sports physics
- Investigate bobsledding techniques and weight optimization strategies
USEFUL FOR
Physics students, sports scientists, engineers, and anyone interested in the mechanics of sledding and bobsledding performance.