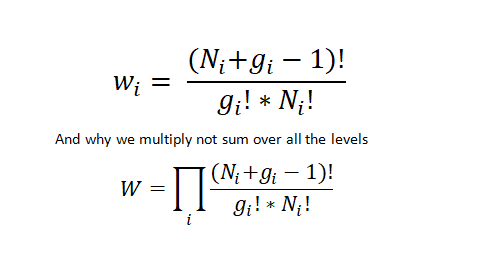Question in Bose-Einstein statistics

Click For Summary
SUMMARY

The discussion clarifies the formula for arranging ni indistinguishable bosons in gi degenerate states, which is given by the equation w_i = (N_i + g_i - 1)! / (g_i!)(N_i - 1)!. This formula is derived from the combinatorial "Stars and Bars" theorem, as bosons are indistinguishable particles. The necessity of dividing by ni! and gi! is explained through the context of particle ensembles, where multiple groups of particles can occupy the same state.

PREREQUISITES
  • Understanding of Bose-Einstein statistics
  • Familiarity with combinatorial mathematics, specifically the Stars and Bars theorem
  • Basic knowledge of particle physics and indistinguishable particles
  • Awareness of probability theory, particularly concepts from William Feller's works
NEXT STEPS
  • Study the "Stars and Bars" theorem in combinatorics
  • Explore Bose-Einstein statistics in depth
  • Read "An Introduction to Probability" by William Feller
  • Investigate applications of Bose-Einstein statistics in quantum mechanics
USEFUL FOR

Students and researchers in physics, particularly those focusing on statistical mechanics, quantum mechanics, and combinatorial mathematics.

patric44
Messages
308
Reaction score
40
Homework Statement
why the number of ways to arrange ni particles in gi degenerate states is = (gi+ni-1) ?
Relevant Equations
(gi+ni-1)
iam not getting why in bose statistics the number of ways to arrange ni particles in gi degenerate states is = (gi+ni-1) ?
and why do we divide by ni factorial , and gi factorial .
bose.png
 
Physics news on Phys.org
The formula is wrong. The correct number of arrangements are:
##w_i= (N_i + g_i -1)!/(g_i !)(N_i-1)! ##
This can be seen in number of ways. It is variant of Star and barn problem of combinatorics since bosons are indistinguishable. Wikipedia article explains it in detail and also it's variant. See https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics) .Alternatively,see the masterpiece book on probability: An introduction to Probability by William Feller,the person who devised this method. To answer why we multiply,it is because we are considering an ensemble of particles. A particular particle group can occupy any given state,another can occupy any given state(It may be same as 1st particle group since they are bosons).
 

Similar threads

Thermal Physics: Photon Statistics on Bose Particles
  • · Replies 1 ·
Replies
1
Views
2K
Graduate Mixed quantum state of the Bose-Einstein distribution
  • · Replies 3 ·
Replies
3
Views
892
Is there a "critical temperature" for 2D Boson gas?
  • · Replies 1 ·
Replies
1
Views
2K
Does Bose Condensation Occur in 2D?
  • · Replies 1 ·
Replies
1
Views
4K
Undergrad Bose-Einstein statistics for μ>ε
  • · Replies 1 ·
Replies
1
Views
1K
What are the expansions of Bose functions for studying thermodynamic behavior?
  • · Replies 2 ·
Replies
2
Views
2K
No bose-Einstein condensate for a 2-d gas, how to prove it?
  • · Replies 2 ·
Replies
2
Views
3K
Deriving Fermi-Dirac Distribution misunderstanding
  • · Replies 1 ·
Replies
1
Views
2K
How to move from the space of moments to the space of energies?
  • · Replies 4 ·
Replies
4
Views
663
What Are the Conditions for Bose-Einstein Condensation to Occur?
  • · Replies 2 ·
Replies
2
Views
2K