oneplusone
- 127
- 2
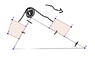
The coefficient of friction between a 3 kg block resting on a flat table, is 0.400. A 5 kg mass is hanging off the table attached to the first mass by a lightweight rope on a frictionless pulley. The system starts at rest. What is the speed of the 5 kg ball when it has fallen 1.5 m.
Solution is attached.
I don't get solution at all. Where are they choosing the reference point for gravity? Can someone just briefly explain. I've been stuck on this for the last half an hour, and am just getting more confused.
Thanks :)
Also, if this is suppose to go in the homework forum (i debated where to put it), please move it there. Sorry in advance.
Solution is attached.
I don't get solution at all. Where are they choosing the reference point for gravity? Can someone just briefly explain. I've been stuck on this for the last half an hour, and am just getting more confused.
Thanks :)
Also, if this is suppose to go in the homework forum (i debated where to put it), please move it there. Sorry in advance.