Quick induced current from magnetic field question direction of current?
- Thread starter michaelw
- Start date
Click For Summary
SUMMARY
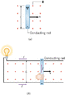
The direction of induced current in a moving rod within a magnetic field is determined by the Right Hand Rule (RHR-1) and Lenz's Law. When the rod moves to the right in a magnetic field directed into the page, the Lorentz force acts upwards on positive charges, resulting in a counterclockwise current. This occurs because the induced current aims to counteract the increasing magnetic flux within the loop, as dictated by Lenz's Law. Thus, the overall current flows counterclockwise, with negative electrons moving downward in the rod.
PREREQUISITES- Understanding of the Right Hand Rule (RHR-1) for electromagnetic induction
- Familiarity with Lorentz force and its application in magnetic fields
- Knowledge of Lenz's Law and its implications for induced currents
- Basic concepts of magnetic flux and its relation to current direction
- Study the application of the Lorentz force in various electromagnetic scenarios
- Explore detailed examples of Lenz's Law in different circuits
- Learn about the mathematical formulation of magnetic flux and its calculations
- Investigate practical applications of induced currents in electrical engineering
Students of physics, electrical engineers, and educators looking to deepen their understanding of electromagnetic induction and the behavior of currents in magnetic fields.
Similar threads
- · Replies 1 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 7 ·
- · Replies 3 ·