- #1
- 10,437
- 1,600
The following diagram and approach illustrates my recent thinking and revisiting on some of the calculations for the radial tidal forces and perhaps even the "force" during a flyby.
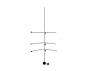
Suppose we consider a series of geodesics , all flying by our massive object M, at points a, b, c,...z on a radial line outwards. Point z is far enough out in space where we consider it to be experiencing negligible gravity. See attached for a diagram.
Now, using the geodesic deviation equations, we can calculate the relative acceleration of geodesic a relative to b. And the relative acceleration of b relative to c, and c relative to d.
We'll call this just the "relative radial acceleration".
If space-time were flat, we could just add up all these differential accelerations to get the acceleration of a relative to z, and hence our "force". We can try to do it in curved space-time as well. For starters, we'll assume that the time dilation at the point of closest approach, point 'a', is negligible in terms of the desired accuracy, and similarly that we're far enough away from M that the change in Schwarzschild r is approximately equal to the distance within desired accuracy. However, we'll see that spatial curvature enters our calculations...
We'll use frame-fields, so that we'll have a locally Minkowskian space-time around points a,b, etc, with a Riemann \hat{R}. We will NOT boost the frame fields. The frame-fields will be the frame-fields of an observer "at rest" in our schwarzschild geometry. (At rest relative to the time-like killing vector field that's also hypersurface orthogonal to be annoyingly exact.)
Note that we'll always use said local basis vectors, so our Riemann will always be wearing a hat. Sometimes formatting issues might make it appear otherwise, for which I apologize in advance.
The basis vectors of our frame field will be unit vectors \hat{r}, \hat{\theta}, \hat{\phi}, \hat{t}. Then we can use the geodesic deviation equation to write:
relative radial acceleration = \hat{R}_{abcd} \: v^{b} \left(\Delta r \right)^{c} v^{d}
Note that we are discarding any components of the above relative acceleration vector except for the radial component.
Here v is the 4-velocity of our observer in the local frame field. Since g^{uv} has diagonal elements of +/- 1 in our frame-field, we don't have to worry about raising or lowering the indexes, except for the sign issues.
The values of the Riemann that are non-zero are \hat{R}_{r \theta r \theta} = \hat{R}_{r \phi r \phi} = +1, \hat{R}_{\theta\phi\theta\phi} = -2, \hat{R}_{rtrt} = +2, \hat{R}_{\theta t \theta t} = \hat{R}_{\phi t \phi t} = -1 all multiplied by m/r^3.
If our motion is in the \hat{\theta} direction, v^{\hat{\theta}} = \beta \gamma and v^{\hat{t}} = \gamma.
\hat{R}_{r \theta r \theta} gives a contribution of \beta^2 \, \gamma^2 \, \Delta r \, m / r^3 to the relative radial acceleration
and
\hat{R}_{rtrt} gives a contribution of 2 \, \gamma^2 \, \Delta r \, m / r^3 to the relative radial acceleration.
We can see that the first term is significant - and we can interpret it as being due to the curvature of space, since \hat{R}_{r \theta r \theta} is part of the topogravitic tensor in the Bel decomposition. It's part of the topogravitic tensor because it contributes a term proportional to \beta^2 to the acceleration, which is just what one expects from a spatial curvature. I.e It's conceptually rather similar to the centripetal/ centrifugal force mv^2 / R of a body moving in a circle of radius R, (where R here has nothing to do with the r in the diagram in spite of the similarity of the name).
Now, this contradicts our initial assumption - that space and space-time was flat. But now we can see how and where the curvature of space (specifically the curvature of space in the particular frame-field we have chosen) affects our force.
Our end result for the relative radial acceleration (i.e. between a and b on our diagram below) is \gamma^2 \, \Delta r \, \left(2m/r^3\right) \left(1 + \beta^2/2\right)
If we integrate over \Delta r, and we take the Newtonian limit we'd get \gamma^2 (m/r^2) (1 + \beta^2/2) for the relative acceleration from a to infinity along the specified radial path. Which seems as good a path as any, as the moving and stationary observers will both have similar notions about simultaneity, as it's at right angles to the direction of motion.
So we can see that the factor of \gamma^2 comes in as we would more or less expect, and that we also have some additional, extraneous factors due to space-curvature.
I haven't addressed the important issue of how the "force" in question transforms,which in my mind is really crucial in determining if one really thinks of it as a force. At this point I'm still thinking about that issue. Nor have I addressed possible issues related to the path definition for the integration to infinity, though the path chosen seems like a reasonable one, perhaps even the "obvious" one.
Suppose we consider a series of geodesics , all flying by our massive object M, at points a, b, c,...z on a radial line outwards. Point z is far enough out in space where we consider it to be experiencing negligible gravity. See attached for a diagram.
Now, using the geodesic deviation equations, we can calculate the relative acceleration of geodesic a relative to b. And the relative acceleration of b relative to c, and c relative to d.
We'll call this just the "relative radial acceleration".
If space-time were flat, we could just add up all these differential accelerations to get the acceleration of a relative to z, and hence our "force". We can try to do it in curved space-time as well. For starters, we'll assume that the time dilation at the point of closest approach, point 'a', is negligible in terms of the desired accuracy, and similarly that we're far enough away from M that the change in Schwarzschild r is approximately equal to the distance within desired accuracy. However, we'll see that spatial curvature enters our calculations...
We'll use frame-fields, so that we'll have a locally Minkowskian space-time around points a,b, etc, with a Riemann \hat{R}. We will NOT boost the frame fields. The frame-fields will be the frame-fields of an observer "at rest" in our schwarzschild geometry. (At rest relative to the time-like killing vector field that's also hypersurface orthogonal to be annoyingly exact.)
Note that we'll always use said local basis vectors, so our Riemann will always be wearing a hat. Sometimes formatting issues might make it appear otherwise, for which I apologize in advance.
The basis vectors of our frame field will be unit vectors \hat{r}, \hat{\theta}, \hat{\phi}, \hat{t}. Then we can use the geodesic deviation equation to write:
relative radial acceleration = \hat{R}_{abcd} \: v^{b} \left(\Delta r \right)^{c} v^{d}
Note that we are discarding any components of the above relative acceleration vector except for the radial component.
Here v is the 4-velocity of our observer in the local frame field. Since g^{uv} has diagonal elements of +/- 1 in our frame-field, we don't have to worry about raising or lowering the indexes, except for the sign issues.
The values of the Riemann that are non-zero are \hat{R}_{r \theta r \theta} = \hat{R}_{r \phi r \phi} = +1, \hat{R}_{\theta\phi\theta\phi} = -2, \hat{R}_{rtrt} = +2, \hat{R}_{\theta t \theta t} = \hat{R}_{\phi t \phi t} = -1 all multiplied by m/r^3.
If our motion is in the \hat{\theta} direction, v^{\hat{\theta}} = \beta \gamma and v^{\hat{t}} = \gamma.
\hat{R}_{r \theta r \theta} gives a contribution of \beta^2 \, \gamma^2 \, \Delta r \, m / r^3 to the relative radial acceleration
and
\hat{R}_{rtrt} gives a contribution of 2 \, \gamma^2 \, \Delta r \, m / r^3 to the relative radial acceleration.
We can see that the first term is significant - and we can interpret it as being due to the curvature of space, since \hat{R}_{r \theta r \theta} is part of the topogravitic tensor in the Bel decomposition. It's part of the topogravitic tensor because it contributes a term proportional to \beta^2 to the acceleration, which is just what one expects from a spatial curvature. I.e It's conceptually rather similar to the centripetal/ centrifugal force mv^2 / R of a body moving in a circle of radius R, (where R here has nothing to do with the r in the diagram in spite of the similarity of the name).
Now, this contradicts our initial assumption - that space and space-time was flat. But now we can see how and where the curvature of space (specifically the curvature of space in the particular frame-field we have chosen) affects our force.
Our end result for the relative radial acceleration (i.e. between a and b on our diagram below) is \gamma^2 \, \Delta r \, \left(2m/r^3\right) \left(1 + \beta^2/2\right)
If we integrate over \Delta r, and we take the Newtonian limit we'd get \gamma^2 (m/r^2) (1 + \beta^2/2) for the relative acceleration from a to infinity along the specified radial path. Which seems as good a path as any, as the moving and stationary observers will both have similar notions about simultaneity, as it's at right angles to the direction of motion.
So we can see that the factor of \gamma^2 comes in as we would more or less expect, and that we also have some additional, extraneous factors due to space-curvature.
I haven't addressed the important issue of how the "force" in question transforms,which in my mind is really crucial in determining if one really thinks of it as a force. At this point I'm still thinking about that issue. Nor have I addressed possible issues related to the path definition for the integration to infinity, though the path chosen seems like a reasonable one, perhaps even the "obvious" one.
Attachments
Last edited: