Radiant intensity of a Lambertian surface

[dougy]

Hello everyone.

From what I've understood, the radiant intensity of a surface is defined as the number of photons emitted by the surface per unit solid angle (steradian) and per second, times a constant (that constant being the mean energy of a photon emitted by this surface). So radiant intensity is expressed in W·sr−1

The way I see it, the radiant intensity of a Lambertian surface (i.e. an isotropic source) is the same in every direction, so plotting the radiant intensity of such a surface for each direction should give in 3D a sphere (or a semisphere) with the source at the center, and in 2D a circle (or a semicircle) with the source at the center. Yet all the representations I find of the radiant intensity of an isotropic source are similar to this one :

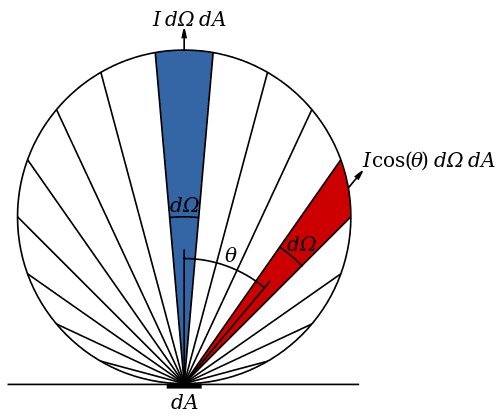
which, the way I see it, would mean that the radiant intensity is maximum in the direction normal to the emitting surface, and approach zero as the direction becomes parallel to the surface.

What am I not getting there?

 

[Andy Resnick]

Perhaps you are not accounting for the cos(q) term- dA*cos(q) is the apparent area of dA, as determined by the angle between the surface normal and the propagation direction.

Here's how I describe a Lambertian emitter (which is not an isotropic emitter) such as a piece of paper or the surface of the moon: each area element dA appears as dA*cos(q). Since the radiant intensity of the Lambertian surface is given by I cos(q)dAdW , the irradiance I/dA = I cos(q) dAdW/dA*cos(q) = I dW and is independent of the orientation of the surface with respect to propagation direction: the lunar surface appears flat, not curved.

Does that help?

 

[Claude Bile]

Hi Dougy,

The radiant intensity is not constant, it is proportional to cos(theta) for a Lambertian emitter. Lambertian emitters have a constant radiance (W/sr/m^2).

Claude.