- #1
leojun
- 26
- 0
which formula is correct?
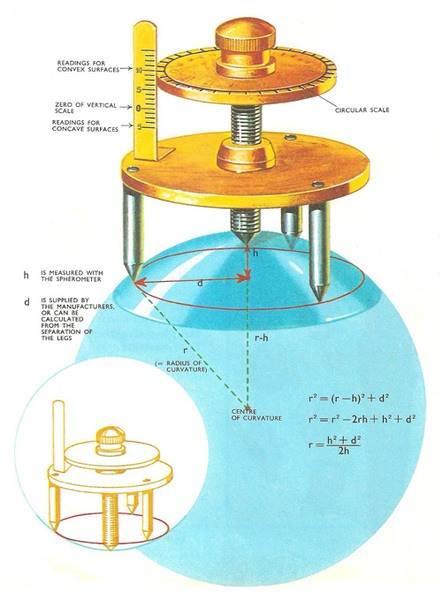or
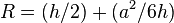
The one of the picture looks correctly derived. Where does the other one come from, and what is "a"?leojun said:
A.T. said:
I see no "b" in the first formula.leojun said:
SORRY,"a" in the second formula is the same as "d" in the first formulaA.T. said:
"a" is the side length of the triangle, or distance between two of the three points.A.T. said:
I don't think so. I think Bystander is right and the formulas are equivalent.leojun said:
A spherometer is a scientific instrument used to measure the radius of curvature of a spherical surface. It consists of a central stem with three or more arms extending from it, each with a small spherical foot at the end.
A spherometer works by measuring the distance between the three or more feet on its arms when placed on a curved surface. By measuring this distance, along with the known distance between the central stem and the feet, the radius of curvature of the surface can be calculated using a mathematical formula.
Measuring the radius of curvature is important in various scientific fields such as optics, astronomy, and materials science. It allows researchers to determine the shape and quality of curved surfaces, which can affect the performance and accuracy of instruments and devices.
The unit of measurement for radius of curvature is typically meters (m) or millimeters (mm), depending on the size of the surface being measured. In some cases, the unit of curvature may also be expressed in diopters (D), which is a unit of measurement for the refractive power of lenses.
No, there are other methods for measuring radius of curvature such as using a radius gauge, a spherometer attachment for a micrometer, or a profilometer. However, a spherometer is a commonly used and accurate instrument for measuring the radius of curvature of curved surfaces.