- #1
DuckAmuck
- 236
- 40
I am simulating random angles from 0 to 2π with a uniform distribution. However, if I take the differences between random angles, I get a non-uniform (monotonically decreasing) distribution of angles.
In math speek:
Ai = uniform(0,2π)
dA = Ai - Aj
dA is not uniform.
Here is a rough image of what I'm seeing. P is probability density:
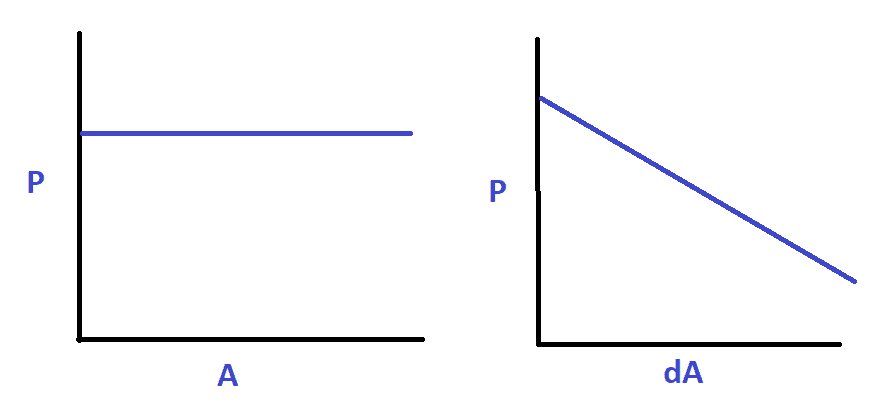 This does not make sense to me. As it seems to imply that the difference between random angles is more likely to be 0 than to be non-zero. You would think it would be uniform, as one angle can be viewed as the *zero* and the other as the random angle. So dA seems like it should also be uniform. What is going on here?
This does not make sense to me. As it seems to imply that the difference between random angles is more likely to be 0 than to be non-zero. You would think it would be uniform, as one angle can be viewed as the *zero* and the other as the random angle. So dA seems like it should also be uniform. What is going on here?
In math speek:
Ai = uniform(0,2π)
dA = Ai - Aj
dA is not uniform.
Here is a rough image of what I'm seeing. P is probability density: