Range of an object launched on a downward hill

[phantomvommand]

Homework Statement

An object is launched from the top of a hill, where the ground lies an angle ϕ below
the horizontal. Show that the range of a projectile is maximized if it is launched along the angle
bisector of the vertical and the ground.

Relevant Equations

Solution I am asking about uses features of a parabola, although this problem is also solvable through kinematics.

I managed to solve this by tilting the axes along the hill, and calculating the range, and then differentiating wrt $\theta$ (angle launched from hill) to get the answer. However, I recently came across the alternative solution below:
The parabola it refers to represents the parabolic envelope of all possible trajectories when launched from the hill.

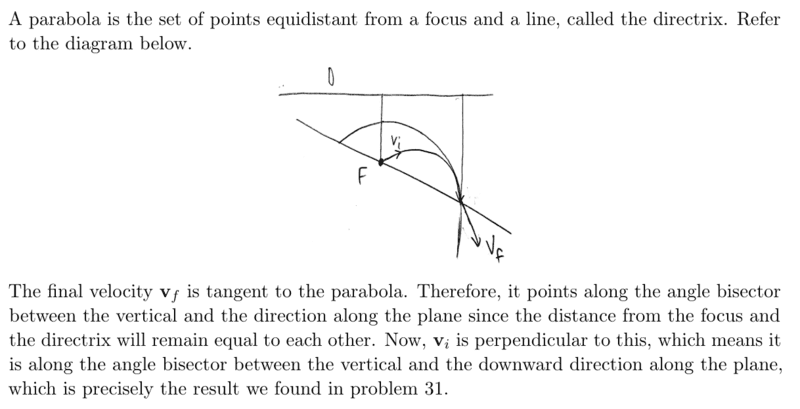
I understand that $v_{f}$ is tangent to the parabola. However, why must it point along the angle bisector between the vertical and the direction along the plane? The remaning claims are understandable for me too.

 

[anuttarasammyak]

An interesting problem. I would like to follow your answer.
x=v_{0x}t
y=v_{0y}t-\frac{g}{2}t^2
x coordinate of contact point on the slope y=-tan $\alpha$ is
\frac{2v_0^2}{g}\cos^2\theta(tan\theta+tan\alpha)
differentiating it with \theta and make it zero
\theta=\frac{\pi}{4}-\frac{\alpha}{2}
or as we wish
\theta+\alpha=\frac{\frac{\pi}{2}+\alpha}{2}
This bisect property holds at contact point thinking of reverse motion. Familiar $\theta$=45 degree for a horizontal plane is included in the solution.
I share with you a curiosity to know how envelope, directrix play a role here.

 

[Lnewqban]

 

[Lnewqban]

Note that the maximum range for horizontal surface is achieved at 45° for the Vi vector.
Please, see:
https://www.physicsclassroom.com/mmedia/vectors/mr.cfm

In the case of our hill, the maximum range is possible for the same angle of 45° for the Vi vector, but respect to the surface of the hill.
Therefore, Vi and Vf vectors should remain perpendicular to each other, regardless the value of the angle Phi.

 

[haruspex]

why must it point along the angle bisector between the vertical and the direction along the plane?

Clearly that is not true in general (consider firing it straight upwards). It is true if the range is maximised, but I see no attempt to use that it is maximised. So I suspect whoever wrote the proof copied and abbreviated it without understanding it, or is relying on something established earlier.

 

[phantomvommand]

It is true if the range is maximised, but I see no attempt to use that it is maximised.

The question does ask for the angle of launch so as to maximise range, so it is definitely relevant. But why is it that for the trajectory that gives maximum range, its velocity upon landing is along the angle bisector of the hill and the vertical to the directrix?

 

[haruspex]

The question does ask for the angle of launch so as to maximise range, so it is definitely relevant. But why is it that for the trajectory that gives maximum range, its velocity upon landing is along the angle bisector of the hill and the vertical to the directrix?

Let me try to be clearer.
I am saying that since the velocity only bisects that angle when the range is maximised, a proof that it is bisected must make use of the condition that the range is maximised. The text you posted does not do that, so the 'proof' is incomplete.
As to how one proves it, I'm not there yet.

 

[phantomvommand]

Let me try to be clearer.
I am saying that since the velocity only bisects that angle when the range is maximised, a proof that it is bisected must make use of the condition that the range is maximised. The text you posted does not do that, so the 'proof' is incomplete.
As to how one proves it, I'm not there yet.

I certainly think that there is some confusion here. I believe that the outline of the proof of the author is as such:
1. Consider the envelope of possible trajectories from a launch point.
2. When range is maximised, Vf is tangent to the envelope of possible trajectories. Because of this, Vf somehow bisects the angle between the hill and the vertical to the directrix of the envelope. <-- I do not understand how the previous fact that Vf is tangent to the envelope proves that it bisects.
3. Vf is perpendicular to Vi (this is proved in a previous part of the problem).
4. As such, Vi must bisect the angle between the hill and the vertical.

 

[Lnewqban]

The question does ask for the angle of launch so as to maximise range, so it is definitely relevant. But why is it that for the trajectory that gives maximum range, its velocity upon landing is along the angle bisector of the hill and the vertical to the directrix?

I believe it is clearly explained (for the horizontal land case) in the link in post #4 above.
Please, read it when you have time.

Adapting that concept for a vertical parabola to the hill (sloped surface), I have graphically shown in the diagram of the same post that vector Vi bisects a-a, as much as Vf does it to d-d.

Copied from that link:
"The range of a projectile is determined by two parameters - the initial value of the horizontal velocity component and the hang time of the projectile. As can be seen from the animation, the projectile launched at 60-degrees has the greatest hang time; yet its range is limited by the fact that the Vx is the smallest of all three angles. The projectile launched at 30-degrees has the greatest Vx of all three launch angles; yet its range is limited by the fact that the hang time is so short. The projectile launched at 45-degree does not win in either category, yet the fact that it is able to place a strong showing in each category contributes to its ability to achieve the greatest range."

 

[phantomvommand]

I believe it is clearly explained (for the horizontal land case) in the link in post #4 above.
Please, read it when you have time.

Adapting that concept to the hill (sloped surface), I have graphically shown in the diagram of the same post that vector Vi bisects a-a, as much as Vf does it to d-d.

Copied from that link:
"The range of a projectile is determined by two parameters - the initial value of the horizontal velocity component and the hang time of the projectile. As can be seen from the animation, the projectile launched at 60-degrees has the greatest hang time; yet its range is limited by the fact that the Vx is the smallest of all three angles. The projectile launched at 30-degrees has the greatest Vx of all three launch angles; yet its range is limited by the fact that the hang time is so short. The projectile launched at 45-degree does not win in either category, yet the fact that it is able to place a strong showing in each category contributes to its ability to achieve the greatest range."

View attachment 345556

I do not agree with your claim that range is maximised when launched at 45 degrees to the hill. The result of the problem suggests that the ideal launch angle is $45 + \frac {\phi} {2}$ away from the hill.

I have since worked out the solution to my own question, and have found that it is a mathematical feature of the parabola where every tangent bisects the angle formed by the vertical to the directrix and the line to the focus.

Your graph in #4 contains some errors too, I believe. The parabola mentioned in the solution represents the envelope of all possible trajectories, not the parabola of an individual trajectory. Furthermore, the focus (of the envelope of all trajectories) should be also be the launch point.

 

[Lnewqban]

I do not agree with your claim that range is maximised when launched at 45 degrees to the hill.

I have not claimed that.

 

[kuruman]

A projectile's trajectory is optimized when there is only one value of the projection angle at which the quantity under consideration (e.g. horizontal range) is an extremum. In this article (see section "Projection angle optimization") it has been shown that the extremum projection angle is given by $$
\theta_{\text{extr.}}=\frac{\pi}{4}+\frac{\varphi}{2}$$where $\varphi$ is the angle of the position vector with respect to the horizontal at any time. Here, $\varphi$ coincides with the angle of the incline at the specific time when the projectile lands. Note that when $\varphi=0$, i.e. the projectile lands at the launching height, we get the familiar 45° angle.

There is more than enough here to answer the question.

 

[anuttarasammyak]

May we write down what we anticiapate as below ?

Trajectry of projectile with peak O (0,0)
y=-\frac{mg}{4E}x^2
its focus F
F(0, -\frac{E}{mg})
where constant E >0 is sum of kinetic energy and gravity potential energy mgy of projectile. or
E=\frac{1}{2}mV_H^2
where V_H is horizontal constant speed of projectile.

Length of the line segments which extend from F and cut by the trajectory at two ends show maximum range of projectile which has energy E, as for the slope on which the line segment lies.

or

The peak of maximum range projectile trajectory has height of $\frac{V_H^2}{2g}$ above the slope.

I confirm the validity of the last statement by way of post #2. Initial velocity magnitude condition should be interpreted as
v_0^2=2(1+\tan\phi(\tan\phi\pm\sec\phi))\frac{2E}{m}
where $\pm$ corresponds to throwing forward or backward wrt the slope $y=\tan\phi\ x$.