Rank forces according to magnitude: Newton's 2nd/3rd laws

[bornofflame]

Homework Statement

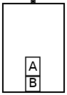
Two crates, A and B, are in an elevator as shown. The mass of crate A is greater than the mass of crate B.

a. The elevator moves downward at constant speed.
...
iii. Rank the forces on the crate according to magnitude, from largest to smallest. Explain your reasoning, including how you used Newton's second and third laws.

Homework Equations

F = ma
W = mg

The Attempt at a Solution

This is what I have:
N (elevator on B) > N (B on A) = N (A on B) = W (Earth on A) = W (Earth on B)
The following ranking is valid because, per Newton's 3rd law, the normal forces between A and B are action-reaction pairs and so are equal in magnitude, which in turn means that, because A is at rest and so has a net force of zero, it's weight, W, is equal in magnitude to the normal of B on A, N (B on A).
Because B is also at rest, relative to the elevator, it's net force is also zero and so the normal force of the elevator on B, N (Elev. on B) is equal in magnitude to the forces in the opposite direction, namely N (A on B) and W (Earth on B).

I believe this is correct but my understanding of the forces is not so solid that I feel I'm 100% confident in this and I am not sure how Newton's 2nd Law plays into the explanation because except for the motion of the elevator, the boxes are not moving and even then the elevator is moving at a constant speed which, to me, speaks more to Newton's 1st law and not the 2nd.
Am I correct in my reasoning or am I missing something?
Thanks for your help.

 

[haruspex]

W (Earth on A) = W (Earth on B)

How did you decide that?

 

[bornofflame]

I was looking at it this way:
if N (A on B) = W (Earth on B),
N (A on B) = N (B on A),
N (B on A) = W (Earth on A)
then W (Earth on A) = W (Earth on B).

Although, now that you've pointed it out, it seems silly because of course they would both have different weights since the mass of B is less than A.

Hmmm.

So, if N (Elevator on B) = N (A on B) + W (Earth on B) then that means that N (A on B) > W (Earth on B)?

 

[haruspex]

if N (A on B) = W (Earth on B)

But it isn't.

So, if N (Elevator on B) = N (A on B) + W (Earth on B) then that means that N (A on B) > W (Earth on B)?

Yes.

 

[bornofflame]

Ok. Thank you, very much!
So, I am pretty sure then that the final ranking is as follows:
N (Elevator on B) > N (B on A) = N (A on B) = W (Earth on A) > W (Earth on B)

Does Newton's 2nd law come into play at all in the explanation? From my understanding it's only the 1st and 3rd laws that are relevant to the explanation.

 

[haruspex]

Ok. Thank you, very much!
So, I am pretty sure then that the final ranking is as follows:
N (Elevator on B) > N (B on A) = N (A on B) = W (Earth on A) > W (Earth on B)

Does Newton's 2nd law come into play at all in the explanation? From my understanding it's only the 1st and 3rd laws that are relevant to the explanation.

Yes, since no momentum is changing in this question.