Ratio of total refelected intensity compared to incident intensity

[Taylor_1989]

Homework Statement

A plane electromagnetic wave is traveling in a vacuum in the positive Z direction and is normally incident on a planar glass of refractive index 1.50 and finite thickness. For normal incidence at a dielectric interface, the reflection and transmission coefficients of intensity are:

$R=\frac{(n_2-n_1)^2}{(n_2+n_1)^2}$

$T=\frac{(4n_1n_2)^2}{(n_2+n_1)^2}$

When the wave enters the glass plate it reflects from both the front and back surfaces of the interface. Considering these two contributions only, show that the total reflected intensity is approximately 7.7% of the incident intensity.

Relevant Equations

Contained within the question

Diagram

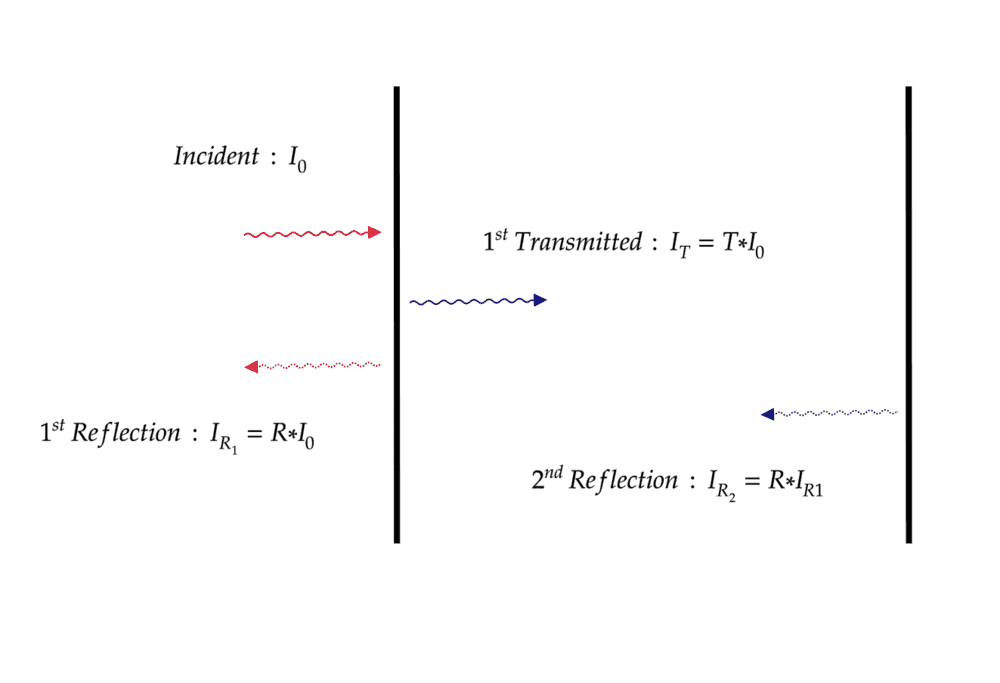
Calculations as follows
$$\frac{I_{total \: Reflection}}{I_{Incident}}=\frac{I_{R_1}+I_{R_2}}{I_0}*100=\frac{R*I_0+(R*T)*I_0}{I_0}$$

Subbing in the relevant equations given in the question

$$\frac{I_{total \: Reflection}}{I_{Incident}}=\frac{(n_2-n_1)^2}{(n_2+n_1)^2}(1+\frac{(4n_1n_2)^2}{(n_2+n_1)^2})*100$$

Now by subbing in the numerical values into my above eqaution I get a percentage of $7.84 \%$ and the question states that it should be $\approx 7.7%$ thus I am not sure my working are correct but can't really understand why as there no other reflection that I can account for, I did think maybe it ment a reflection off the first mirror again but adding that into the above calculations I get $8\%$ which it larger than my original. Have I missed something in my calculation?

 

[hutchphd]

Take a look at your expression for T. R+T=1 always

 

[kuruman]

The transmission coefficient should be $T=\dfrac{4n_1n_2}{(n_2+n_1)^2}$. There is no square term in the numerator, but that's not a problem here. With the correct $T$ I also got 7.8% which is approximately 7.7% of the incident intensity as the problem suggests. I see no problem with your answer other than fixing the typo.

 

[hutchphd]

I see no problem with your answer other than fixing the typo.

This is not a complete and correct answer. The 2nd Reflection light is scattered at the original interface giving rise transmitted and 3rd reflection light and so on ad infinitum.
The good news is that the infinite sum you generate from this is easy to recognize and that leads to the easy solution

 

[kuruman]

This is not a complete and correct answer. The 2nd Reflection light is scattered at the original interface giving rise transmitted and 3rd reflection light and so on ad infinitum.
The good news is that the infinite sum you generate from this is easy to recognize and that leads to the easy solution

Sure, you get a geometric series to add. However, the statement of the problem as posted says

Considering these two contributions only, show that the total reflected intensity is approximately 7.7% of the incident intensity.

 

[hutchphd]

oops sorry. The full problem is much more fun!

 

[kuruman]

oops sorry. The full problem is much more fun!

Yes.

Correction on Edit
In the reflected region,
1. the first reflection has intensity $R$
2. the transmitted ray has intensity $T$, upon reflection off the back surface it has intensity $RT$ and upon transmission through the front surface, it has intensity $RT^2$.
I retract my confirmation in post #3.I made a mistake and my recalculated answer is not 7.84% with these considerations. I think that "approximately" in the statement of the problem does not mean "close to 7.7%" but "close to the answer that one gets when one considers all reflections off the back interface and not just one."

 

[Taylor_1989]

Yes.

Correction on Edit
In the reflected region,
1. the first reflection has intensity $R$
2. the transmitted ray has intensity $T$, upon reflection off the back surface it has intensity $RT$ and upon transmission through the front surface, it has intensity $RT^2$.
I retract my confirmation in post #3.I made a mistake and my recalculated answer is not 7.84% with these considerations. I think that "approximately" in the statement of the problem does not mean "close to 7.7%" but "close to the answer that one gets when one considers all reflections off the back interface and not just one."

Sorry but I am having a issue understanding, for your recalculation for total refection did you have the sum

$$R+RT+RT^2$$

Or did you form a geometric series which was mentioned in post #4.

 

[kuruman]

Sorry but I am having a issue understanding, for your recalculation for total refection did you have the sum

$$R+RT+RT^2$$

Or did you form a geometric series which was mentioned in post #4.

I had the sum $R+RT^2$. My initial attempt did not correctly take into account the transmission through the front surface of the secondary reflections. Note that the secondary reflections must all have the same $T^2$ factor because they are all transmitted through the front boundary twice; they differ in the number of internal reflections which increases by two from one to the next starting with the first secondary reflection. Can you figure out the series?

On edit
It would be instructive to add the infinite series for the reflected and the transmitted part, add the two and see if the sum is 1. I did it and it is.