MHB Real world trigonometry problem making furniture

Click For Summary
SUMMARY

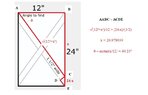
The discussion centers on solving a trigonometric problem related to furniture construction, specifically a bed bench. The user seeks to determine the angles required to cut a board that bisects a rectangle, ensuring the board intersects the rectangle in a specific manner. The problem involves known dimensions of both the rectangle and the parallelogram. Visual aids, such as diagrams, are utilized to clarify the geometric relationships involved.

PREREQUISITES
  • Understanding of basic trigonometry concepts, including sine, cosine, and tangent.
  • Familiarity with geometric shapes, specifically rectangles and parallelograms.
  • Ability to interpret and create geometric diagrams.
  • Knowledge of angle measurement and cutting techniques in woodworking.
NEXT STEPS
  • Research trigonometric functions and their applications in woodworking.
  • Learn about geometric constructions involving rectangles and parallelograms.
  • Explore tools for calculating angles and dimensions, such as CAD software.
  • Investigate techniques for accurately cutting angles in wood based on trigonometric calculations.
USEFUL FOR

Woodworkers, furniture designers, and anyone involved in DIY projects requiring precise angle measurements and cuts in geometric shapes.

shane3
Messages
1
Reaction score
0
I'm building a bed bench and I have an interesting trig problem that I can't figure out. I have a rectangle with known values and a parallelogram that bisects it with a known width. Like a board. I want to be able to figure out the angles so I can cut it. I want the board to intersect the rectangle in a specific way. I've attached an image as I have no other way to describe this. It feels like this should be solvable. Just not sure how. Any help would be great. Thanks.
View attachment 9223
 

Attachments

  • trigproblem.png
    trigproblem.png
    36.3 KB · Views: 139
Mathematics news on Phys.org
see diagram ...
 

Attachments

  • angle_measure.jpg
    angle_measure.jpg
    28.3 KB · Views: 130

Similar threads

High School Calculating trigonometry without calculator?
  • · Replies 8 ·
Replies
8
Views
2K
High School Compensating for a bias - a simple geometry/algebra problem:
  • · Replies 1 ·
Replies
1
Views
2K
High School How Can Trigonometry Calculate Distances in Surveying?
  • · Replies 5 ·
Replies
5
Views
3K
High School A Simpler Way to Find the Shaded Area?
  • · Replies 1 ·
Replies
1
Views
2K
Is My Understanding of Angular Momentum and Trigonometry Correct?
  • · Replies 3 ·
Replies
3
Views
1K
Undergrad Optimization problem: Error mitigation while using trigonometry
  • · Replies 18 ·
Replies
18
Views
3K
Finding the Distance to a Building with Trigonometry
  • · Replies 4 ·
Replies
4
Views
3K
MHB How Can I Efficiently Cut Wood Boards of Different Lengths?
  • · Replies 4 ·
Replies
4
Views
4K
MHB How do I calculate the side of a rhombus using the bisector of an angle theorem?
  • · Replies 1 ·
Replies
1
Views
2K
MHB Determine the Number of Real Roots
  • · Replies 2 ·
Replies
2
Views
3K