Refraction Angle: Find the Answer to Your Question

[StudentofPhysics]

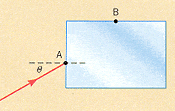
The drawing shows a rectangular block of glass (n = 1.52) surrounded by liquid carbon disulfide (n = 1.63). A ray of light is incident on the glass at point A with a = 46.0° angle of incidence. At what angle of refraction does the ray leave the glass at point B?

I know to use n1 sin 01 = n2 sin 02 (0 = theta)

i came up with 50.48 degrees, which was wrong. Then I figured since it was traveling back out of the block, maybe i should keep going and solve for that angle, which just cam out to be 46 degrees, also wrong.

What am I doing wrong?

 

[quasar987]

i came up with 50.48 degrees, which was wrong. Then I figured since it was traveling back out of the block, maybe i should keep going and solve for that angle, which just cam out to be 46 degrees, also wrong.

50.48° is the angle at which the ray emerges in the block. It then continues its course and hits the surface block-liquid at the angle 90° - 50.48° = 39.52° (draw a little square-triangle to see it). Then you got to run another n1 sin 01 = n2 sin 02 to find the angle 02 at which the ray emerges in the liquid. But this time, of course, the index "1" refers to the glass and the index "2" refers to the liquid.

 

[StudentofPhysics]

Thank you. I forget to subtract 50.48 from 90 before continuing on.
Got it now though.