SUMMARY
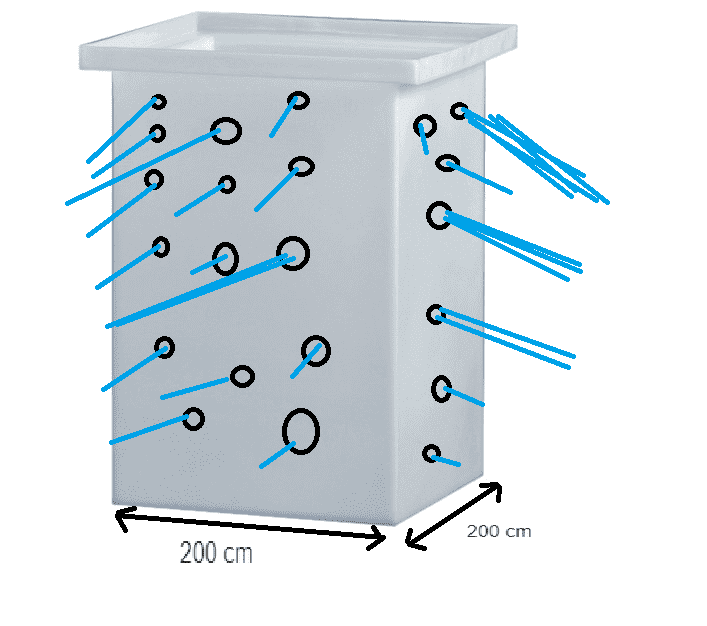
The discussion centers on a related rates calculus problem involving a rectangular water tank with a base length of 200 cm and 100 holes for water outflow. The task is to determine the flow rate from each hole, considering a measurement error in the water height of ±1 cm. The problem was initially perceived as incomplete but was later clarified, allowing for a solution to be found. The interaction highlights the importance of clear problem statements in calculus applications.
PREREQUISITES
- Understanding of related rates in calculus
- Familiarity with differential equations
- Knowledge of flow rate concepts
- Basic geometry of rectangular prisms
NEXT STEPS
- Study related rates problems in calculus
- Explore differential equations applications in fluid dynamics
- Learn about flow rate calculations in physics
- Review geometric properties of prisms and their implications in volume calculations
USEFUL FOR
Students studying calculus, educators teaching related rates, and anyone interested in applying mathematical concepts to real-world fluid dynamics problems.