burian
- 64
- 6
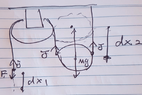
> The set up: At left end, the rope is pulled down with a distance $dx_1$ by a force of constant magnitude $F$, the mass of $M$ is wrapping around by rope on the right and moves up by a distance $dx_2$ due to this. Problem: Find relate the two displacements.
I thought of applying energy conservation, we put in energy $Tdx_1$ into the system and we add up the energy induced on the rest of the system. Noting that $F=T$,
$$Tdx_1= 2Tdx_2 - Mg dx_2$$
**Explanation for left side** : We input an energy of $F \cdot dx_1$ when we pull the rope by$dx_1$ with force $F$, since $F=T$, the energy is just $T dx_1$
**Explanation for right side :** The mass is pulled up by $dx_2$, this goes into kinetic energy of the body, this kinetic energy can be written using the work energy theorem as the external forces dotted with $dx_2$, $(2T-mg) \hat{j} \cdot (dx_2 \hat{j})= (2T- mg) dx_2$
This simplifies to:
$$ dx_1 = (2- \frac{Mg}{T} ) dx_2 \tag{1}$$
But, if we go by the differential conservation of rope, we find that $dx_1 = 2 dx_2$ is it possible to simplfy eqtn (1) into this, or have I done something conceptually wrong?
I thought of applying energy conservation, we put in energy $Tdx_1$ into the system and we add up the energy induced on the rest of the system. Noting that $F=T$,
$$Tdx_1= 2Tdx_2 - Mg dx_2$$
**Explanation for left side** : We input an energy of $F \cdot dx_1$ when we pull the rope by$dx_1$ with force $F$, since $F=T$, the energy is just $T dx_1$
**Explanation for right side :** The mass is pulled up by $dx_2$, this goes into kinetic energy of the body, this kinetic energy can be written using the work energy theorem as the external forces dotted with $dx_2$, $(2T-mg) \hat{j} \cdot (dx_2 \hat{j})= (2T- mg) dx_2$
This simplifies to:
$$ dx_1 = (2- \frac{Mg}{T} ) dx_2 \tag{1}$$
But, if we go by the differential conservation of rope, we find that $dx_1 = 2 dx_2$ is it possible to simplfy eqtn (1) into this, or have I done something conceptually wrong?