Relativistic rocket equation

[greg_rack]

I am studying through online resources some principles of spacecraft propulsion, since it really fascinates me, and makes me want to know a bit more about it :)
For rockets, thruster, I found the Tsiolkovsky rocket equation:
$$\Delta v=v_e ln(\frac{m_0}{m_f})$$

Of course, rockets can travel up to relativistic speeds, thus a relativistic implementation of the RE must be taken into account for a higher degree of accuracy in calculations.
All implementations I found, rely on this equation which gives the mass ratio in terms of $\Delta v$ and exhaust speed $v_e$... but I couldn't manage to derive it, since in all papers it is given without demonstration:

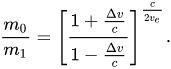
Could you please give me a hint on how to get to this identity?

 

[etotheipi]

I think you can do it like this. Let $v$ be the velocity of the rocket measured in the initial rest frame of the rocket. At some time $t$, the rocket has momentum $p$ and energy $E$. At some later time, after ejecting some amount of mass $dk$, the rocket has mass $m+dm$, momentum $p + dp$ and energy $E + dE$. Note that, unlike energy and momentum, mass is not conserved in this process i.e. $dm \neq - dk$.

If the speed of the ejected mass $dk$ with respect to the spaceship is $u$, then its velocity in the initial rest frame is $\tilde{v}= \dfrac{v-u}{1-uv}$. The ejected mass possesses energy $-dE$ and momentum $-dp$. The change in momentum of the rocket is $dp = d(\gamma m v) = \dfrac{-\tilde{v} dk}{\sqrt{1-\tilde{v}^2}}$ and the change in energy of the rocket is $dE = d(\gamma m) = \dfrac{-dk}{\sqrt{1-\tilde{v}^2}}$. Write\begin{align*}
d(\gamma mv) &= \tilde{v} d(\gamma m) = \dfrac{v-u}{1-uv} d(\gamma m) \\
\implies \frac{d(\gamma mv) }{dv} &= \dfrac{v-u}{1-uv} \dfrac{d(\gamma m)}{dv}
\end{align*}Can you solve this differential equation?

 

[pervect]

I think all one has to do is replace normalized velocity $\beta = v/c$ with rapidity, w.
https://en.wikipedia.org/wiki/Rapidity

Rapidities add in SR, while velocities don't. So, v = at becomes w = a$\tau$.

So, for the non-relativistic case we can say
$$m \frac{dv}{dt} = -v_e \frac{dm}{dt} $$
which reduces to
$$dv = v_e \frac{dm}{m}$$
which gives the solution
$$v =v_e ln \frac{m_i}{m_f}$$

Replacing v by the rapidity w gives:
$$dw = \frac{v_e}{c} \frac{dm}{m}$$
and
$$w = \frac{v_e}{c} ln \frac{m_i}{m_f}$$

where
$$w = \frac{1}{2} ln \frac{1+v/c } {1-v/c }$$
and in the limit when v is small, $w \approx v/c$.

This can be solved to get v as a function of the mass ratio rather than w as a faction of the mass ratio.

Hopefully I didn't make any silly errors, but I won't guarantee it. I wouldn['t be too surprised if I made some error with a factor of c, I usually use geometric units where c=1.

 

[etotheipi]

It is not so hard from first principles, though. From #2, write\begin{align*}
v \frac{d(\gamma m)}{dv} + \gamma m &= \frac{v-u}{1-uv} \frac{d(\gamma m)}{dv} \\

\gamma m &= \left(\frac{v-u}{1-uv} - v \right) \frac{d(\gamma m)}{dv} \\

\gamma m &= \left(\frac{u(v^2-1)}{1-uv} \right) \frac{d(\gamma m)}{dv} \\ \\

\int_{v_1}^{v_2} dv \frac{(1-uv)}{u(v^2-1)} &= \int_{\gamma_1 m_1}^{\gamma_2 m_2} \frac{d(\gamma m)}{\gamma m} \\

\frac{-1}{u} \int_{v_1}^{v_2} dv \frac{1}{1-v^2} - \int_{v_1}^{v_2} dv \frac{v}{v^2-1} &= \int_{\gamma_1 m_1}^{\gamma_2 m_2} \frac{d(\gamma m)}{\gamma m} \\ \\

\frac{-1}{u} \left[ \mathrm{artanh}(v) \right]_{v_1}^{v_2} - \frac{1}{2} \ln{ \left| \frac{v_2^2-1}{v_1^2-1} \right|} &= \ln \left( \frac{\gamma_2 m_2}{\gamma_1 m_1} \right)

\end{align*}Because $v_1, v_2 < 1$, $\frac{1}{2} \ln{ \left| \dfrac{v_2^2-1}{v_1^2-1} \right|} = \dfrac{1}{2} \ln{\left( \dfrac{1-v_2^2}{1-v_1^2} \right)} = \ln{\left( \frac{\sqrt{1-v_2^2}}{\sqrt{1-v_1^2}} \right)} = \ln{ \left( \dfrac{\gamma_1}{\gamma_2}\right)}$. So\begin{align*}

\frac{-1}{u} \left[ \mathrm{artanh}(v_2) - \mathrm{artanh}(v_1) \right] &= \ln \left(\frac{m_2}{m_1} \right) \\

\implies \mathrm{artanh}(v_2) - \mathrm{artanh}(v_1) &= u \ln \left(\frac{m_1}{m_2} \right) \\

w_2 - w_1 &= u \ln \left(\frac{m_1}{m_2} \right)

\end{align*}$w$ is the rapidity