Relativistically invariant 2-body phase space integral

[George Wu]

TL;DR

I encounter a function that I don‘t know in the calculation of Relativistically invariant 2-body phase space integral

I encounter a function that I don‘t know in the calculation of Relativistically invariant 2-body phase space integral:

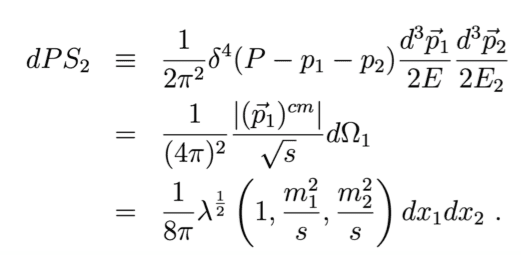
in this equation, $s$is the square of total energy of the system in the center-of-mass frame(I think)
I don't know what the function $\lambda^{\frac{1}{2}}$ is.
There are more equations involving this function:

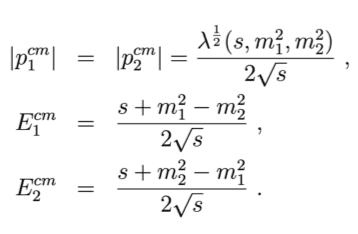
I just want to know if anyone knows which textbook these equations come from, or what the function $\lambda^{\frac{1}{2}}$ is.

 

[dextercioby]

Do you have any reference for those 2 screenshots? A book, some lecture notes we could have access to. Otherwise, I can't recall any special function in mathematics with that notation.

 

[malawi_glenn]

It is called the Källén function https://en.wikipedia.org/wiki/Källén_function

$\lambda^{1/2} (x,y,z)$ is just short-hand for $\sqrt{\lambda (x,y,z) }$

This is a good reference for relativistic particle kinematics https://edu.itp.phys.ethz.ch/hs10/ppp1/PPP1_2.pdf

 

[vanhees71]

A very good review about all the kinematics in relativistic scattering problems can be found in the Review of Particle Physics:

https://pdg.lbl.gov/2022/reviews/rpp2022-rev-kinematics.pdf