Renormalisation of the Fermionic triangle loop

[Ramtin123]

I am trying to renormalise the following loop diagram in the Standard Model:

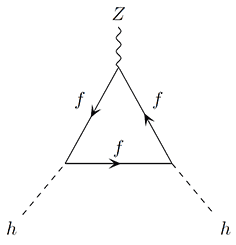
Using the Feynman rules, we can write the amplitude as follows:
$$ \Gamma_f \sim - tr \int \frac{i}{\displaystyle{\not}\ell -m_f}
\frac{i^2}{(\displaystyle{\not}\ell+ \displaystyle{\not}k -m_f)^2}
\frac{d^4 \ell}{(2 \pi)^4} $$
where $k$ and $\ell$ are external Higgs and loop momenta, and $m_f$ being the fermion mass. I have ignored the coefficients coming from vertex factors.
After evaluating the loop integral functions using dimensional regularisation, I ended up with the following expression:
$$ \Gamma_f \sim \frac{m_f}{4 \pi^2}
\left( 3\Delta -6\ln \frac{m_f}{\mu} +4
-6 \sqrt{1-4x} \ \ln \frac{1 +\sqrt{1-4x}}{2\sqrt{x}} \right)$$
The loop integral is clearly divergent due to $\Delta \equiv \ln \pi - \gamma_E + 2/\epsilon$ term, when $\epsilon = 4 -d \to 0$.
Here, $x \equiv (m_f/k)^2$, $d$ is dimension, $\mu$ regularisation scale, and $\gamma_E$ being Euler-Mascheroni constant.
How should I introduce the counter-terms to make the expression for the amplitude finite?

 

[Gavinn]

As always in the books.
Check Srednicki.