dishwasher95
- 10
- 0
Hi,
Say there's a gyroscope with moments of inertia Ix, Iy and Iz spinning around a vertical z-axis (see attached illustration) with a given angular velocity ωz. Notice that the gyroscope is floating in space as in that there's no gravity acting on the gyroscope.
Now I apply a torque τx around the x-axis.
The torque will introduce angular momentum Lx around the x-axis.
What I want to know is, how can I determine the resisting torque τres,x that resists the motion of the applied torque τx?
And what is the size of the torque τy that will occur due to the applied torque τx?
I'm look for an analytical approach to relate the applied torque τx to τy and τres,x.
I feel like I've searched the whole internet for a clear explanation but failed to find one.
If anyone would be willing to go through the theory step-by-step or just show me some literature that does I'd appreciate it immensely!
Attached is also some formulas I found online but I would love a derivation.
Thanks in advance!
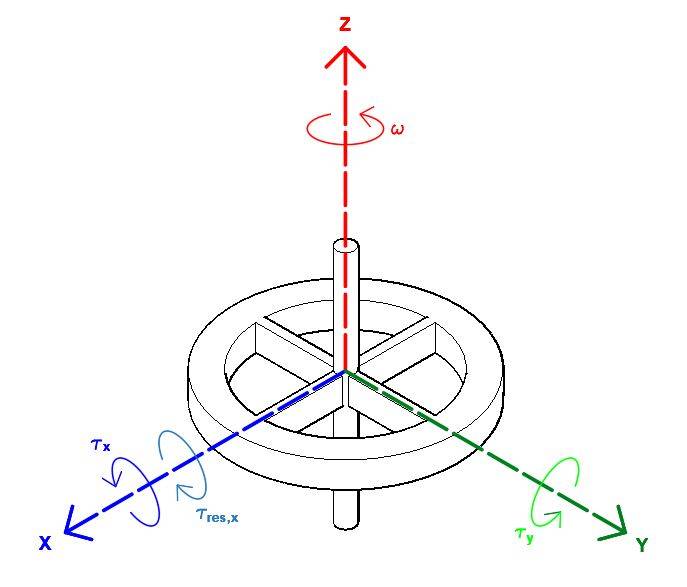

Say there's a gyroscope with moments of inertia Ix, Iy and Iz spinning around a vertical z-axis (see attached illustration) with a given angular velocity ωz. Notice that the gyroscope is floating in space as in that there's no gravity acting on the gyroscope.
Now I apply a torque τx around the x-axis.
The torque will introduce angular momentum Lx around the x-axis.
What I want to know is, how can I determine the resisting torque τres,x that resists the motion of the applied torque τx?
And what is the size of the torque τy that will occur due to the applied torque τx?
I'm look for an analytical approach to relate the applied torque τx to τy and τres,x.
I feel like I've searched the whole internet for a clear explanation but failed to find one.
If anyone would be willing to go through the theory step-by-step or just show me some literature that does I'd appreciate it immensely!
Attached is also some formulas I found online but I would love a derivation.
Thanks in advance!