- #1
johnlpmark
- 17
- 0
- TL;DR Summary
- Rifled bullets are gyroscopes: precession maintains the center of pressure before the center of mass. A side effect is deflection from yawing (aerodynamic jump) and pitching (spin drift). Spinning bullets and gyroscope diagrams show opposite forces.
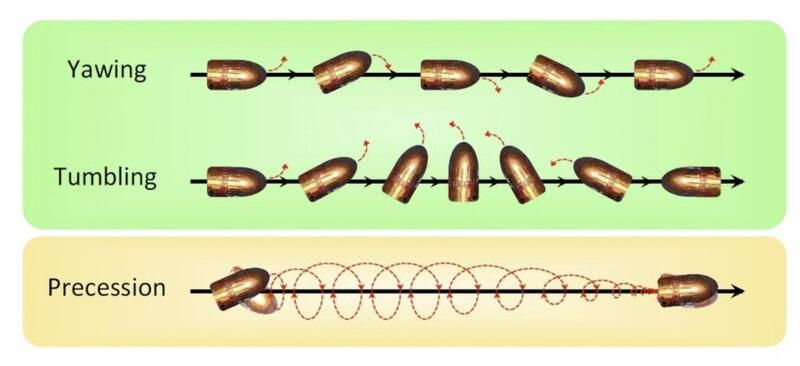
1) Bullet spin causes a bullet to become a gyroscope. Specifically, bullets have their center of pressure in front of their center of mass. Therefore, when pressed, gyroscopic forces cause a bullet to spin 90 degrees instead of tumble. See this diagram:
2)The precession does not cause the bullet to point into the direction of movement, but the direction of apparent incoming wind. That means that if there is a crosswind of 20mph, the bullet will turn slightly to point towards the incoming wind while traveling straight forward. See this diagram:
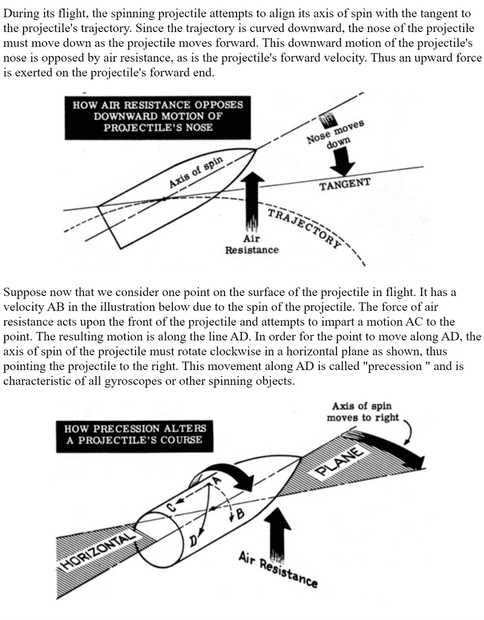
3a) As a bullet drops, there is apparent wind coming from the downward direction. Apparent wind occurs when there is a differential between the object and the surrounding medium. Therefore, the bullet turns down as it drops. See this diagram below.
3b) Importantly, gravity accelerates, so there is always an increasing apparent wind as the bullet falls. This accelerating vertical apparent wind causes continuous forward rotation of the bullet.
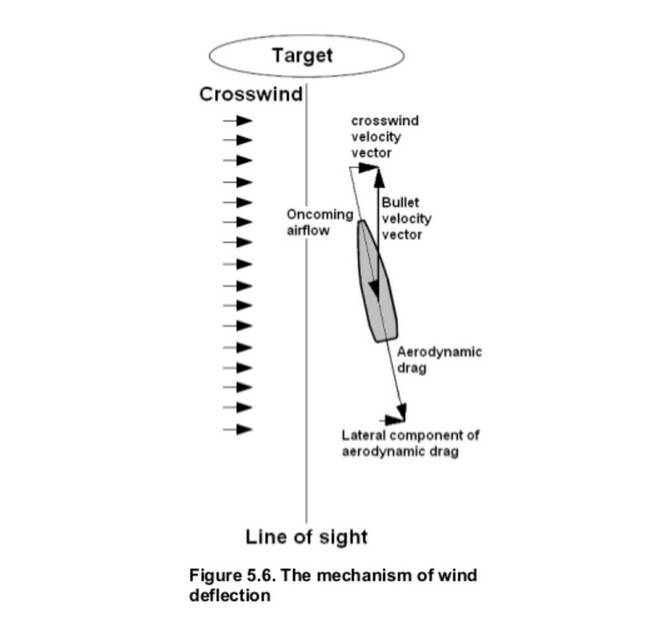
4a) Air resistance forces to the front of the bullet and those to the side of the bullet cause different behavior. Air resistance to the front causes the bullet to reorient into the direction of the incoming force. (See the first image.)
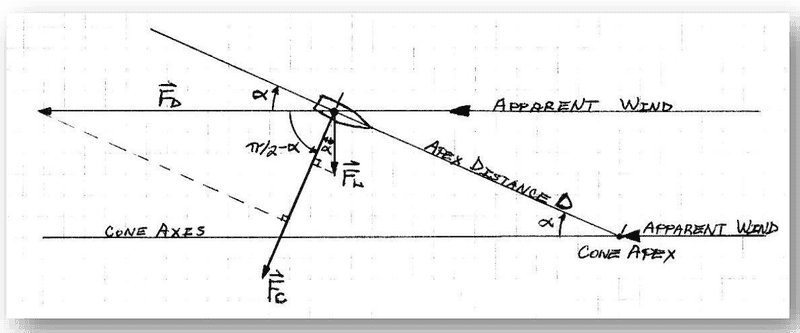
4b)Air resistance to the side of the bullet (i.e., from the left, up, down, or right directions) pushes the bullet to point 90 degrees clockwise to the incoming air. So left-to-right crosswind cause aerodynamic jump down and a or right-to-left crosswind causes aerodynamic jump up. (Note the horizontal defection in this image is due to the crosswind, which is distinct from spin drift.) See this diagram:
[
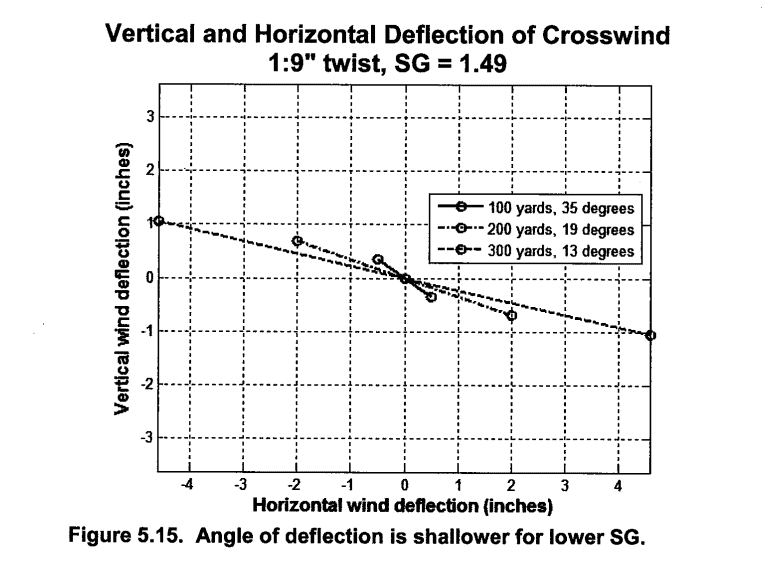
5) Therefore, intuitively, when a bullet rotates down due to being in a falling trajectory with gravity, it points to the right if it has a right-hand twist:
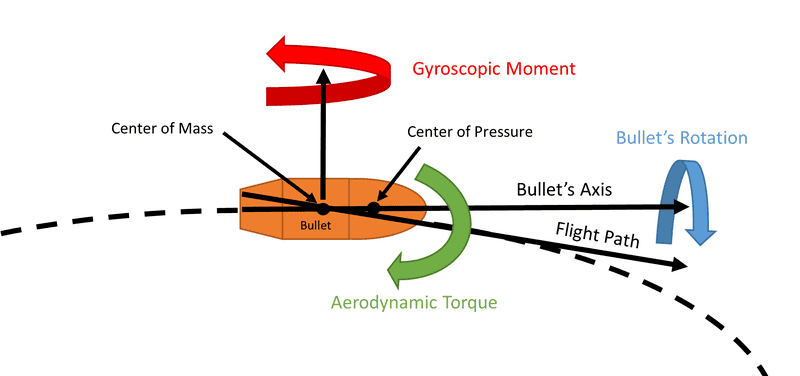
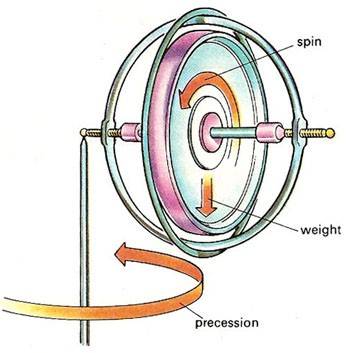
6) But every diagram I see of a gyroscope has the gyroscope rotating the opposite direction.
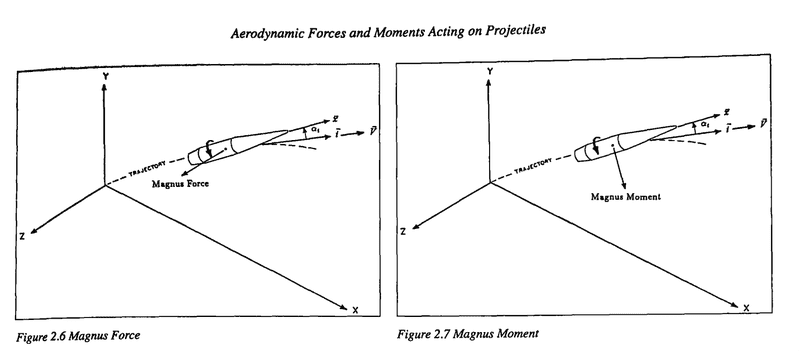
7) I can’t figure out why the bullet gyroscope rotates in the opposite direction of other gyroscopes. This is not Magnus effect! From Modern Exterior Ballistics, McCoy, “Although the Magnus force acting on a spinning projectile is usually small enough to be neglected, the Magnus moment must always be considered.” Note in the diagram that the Magnus moment points down, and not the to left or right. See these diagrams:
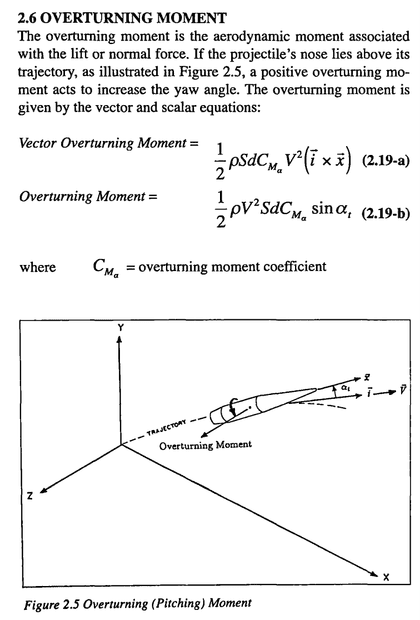
 8) In contrast, spin drift is related to the pitching moment, which does point left or right. See the below diagram. Importantly, bullets do not roll off of air. Indeed, if that were the case, then the rear has more surface area and it would cause the bullet to point away from the incoming air flow which is not the case.
8) In contrast, spin drift is related to the pitching moment, which does point left or right. See the below diagram. Importantly, bullets do not roll off of air. Indeed, if that were the case, then the rear has more surface area and it would cause the bullet to point away from the incoming air flow which is not the case.
9) Something to note is that the traditional depiction of bullet rotation may be somewhat inaccurate. (I cannot confirm.) Traditionally bullets are depicted as rotating around the center or mass. Instead, they may rotate around an independent axis. See this diagram:
Thanks so much for the help!
-John
2)The precession does not cause the bullet to point into the direction of movement, but the direction of apparent incoming wind. That means that if there is a crosswind of 20mph, the bullet will turn slightly to point towards the incoming wind while traveling straight forward. See this diagram:
3a) As a bullet drops, there is apparent wind coming from the downward direction. Apparent wind occurs when there is a differential between the object and the surrounding medium. Therefore, the bullet turns down as it drops. See this diagram below.
3b) Importantly, gravity accelerates, so there is always an increasing apparent wind as the bullet falls. This accelerating vertical apparent wind causes continuous forward rotation of the bullet.
4a) Air resistance forces to the front of the bullet and those to the side of the bullet cause different behavior. Air resistance to the front causes the bullet to reorient into the direction of the incoming force. (See the first image.)
4b)Air resistance to the side of the bullet (i.e., from the left, up, down, or right directions) pushes the bullet to point 90 degrees clockwise to the incoming air. So left-to-right crosswind cause aerodynamic jump down and a or right-to-left crosswind causes aerodynamic jump up. (Note the horizontal defection in this image is due to the crosswind, which is distinct from spin drift.) See this diagram:
[
5) Therefore, intuitively, when a bullet rotates down due to being in a falling trajectory with gravity, it points to the right if it has a right-hand twist:
6) But every diagram I see of a gyroscope has the gyroscope rotating the opposite direction.
7) I can’t figure out why the bullet gyroscope rotates in the opposite direction of other gyroscopes. This is not Magnus effect! From Modern Exterior Ballistics, McCoy, “Although the Magnus force acting on a spinning projectile is usually small enough to be neglected, the Magnus moment must always be considered.” Note in the diagram that the Magnus moment points down, and not the to left or right. See these diagrams:
9) Something to note is that the traditional depiction of bullet rotation may be somewhat inaccurate. (I cannot confirm.) Traditionally bullets are depicted as rotating around the center or mass. Instead, they may rotate around an independent axis. See this diagram:
Thanks so much for the help!
-John