Andrew1955
- 56
- 0
Hi, I read through einsteins popular book on relativity translated into english around 1922 and subsequently read the original 1905 paper on the electrodynamics of moving bodies.
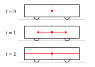
So we have a fixed observer seeing flashes happening at the same time and we have a moving observer seeing one flash after the other. However we know the reason the moving observer sees one flash before the other is because he is moving towards the first flash. By einsteins definition of his experiment the two flashes occur at the same time.
So how do we then get to the conclusion of time passing at different rates?
Yes we can say the observers are confused by their experience due to the motion of the train and the finite speed of light, but it seems clear to me it is a fact the flashes happen at the same time on the train/moving line.
Am i missing something or am I reading too much into the proposed thought experiment which in fact is not so very good at introducing the idea?
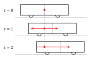
So we have a fixed observer seeing flashes happening at the same time and we have a moving observer seeing one flash after the other. However we know the reason the moving observer sees one flash before the other is because he is moving towards the first flash. By einsteins definition of his experiment the two flashes occur at the same time.
So how do we then get to the conclusion of time passing at different rates?
Yes we can say the observers are confused by their experience due to the motion of the train and the finite speed of light, but it seems clear to me it is a fact the flashes happen at the same time on the train/moving line.
Am i missing something or am I reading too much into the proposed thought experiment which in fact is not so very good at introducing the idea?