Resonant cavity and circuit analysis

[dRic2]

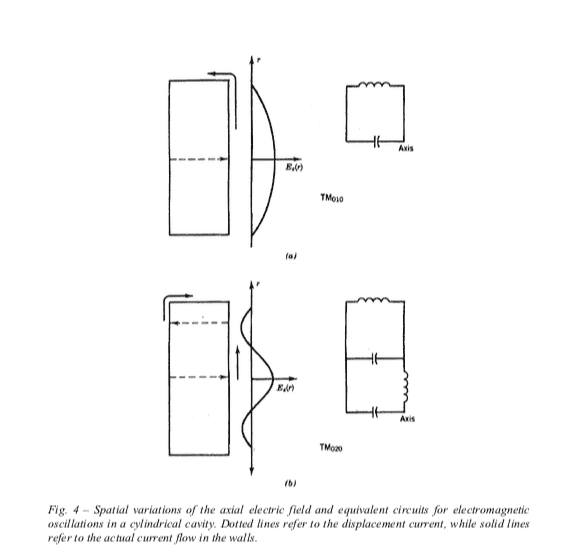
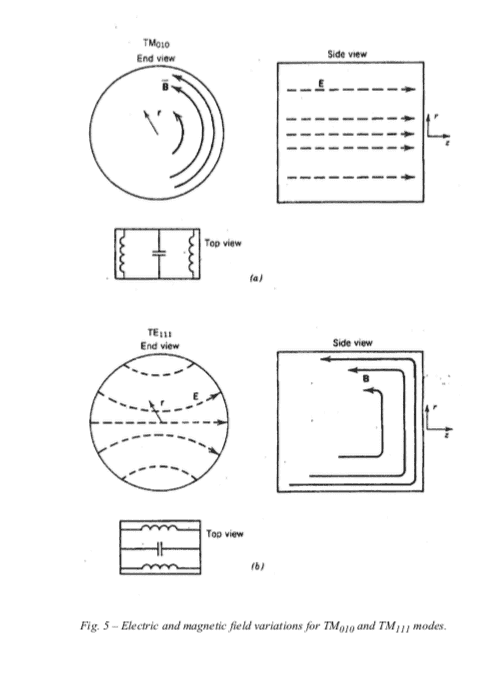
As I understand, if you solve the Maxwell's field equations for a resonant cavity, supposing a time dependence of the form $e^{iwt}$, you get an eigenvalue problem and different modes as possible solutions. I'm reading some notes where the author states that each mode can be associated with a corresponding RCL circuit. Assuming ideal conducting walls you have no resistances (a part from a possible device to which the cavity is coupled), but I don't get how to draw the corresponding circuit for each TM or TE mode. To better explain myself I'll post some pictures:

 

[trurle]

You should start with each extremum of E corresponding to capacitor, and node corresponding to inductor. You will get ladder circuit. Afterward, you need to treat each section of ladder as resonator in primary resonance, and calculate values of L and C. After calculation is complete for each section, produce the equivalent circuit for the frequency of interest. Some sections will reduce to single capacitors, while others - for single inductors.
For example, TM02 will have 11 elements (8 inductors and 3 capacitors) before reduction. Of course, such LC circuit approximation is intrinsically narrowband.

 

[dRic2]

Thanks a lot. But I am pretty weak in both E&M and circuit analysis...

You should start with each extremum of E corresponding to capacitor, and node corresponding to inductor.

Can you explain why this is so?

 

[trurle]

Can you explain why this is so?

Extremum of E corresponds to resonator area with large swings of voltage but low currents. This state is well approximated by capacitor. Opposite is correct for zero of electric field.

 

[dRic2]

low currents

Why do you say that ? I suppose we are talking about induced currents, but I don't see it