- #1
misko
- 46
- 0
I am learning about lasers and trying to clear up some blurry concepts in my head so I am not necessary using heavy math for description here so please bear with me.
Let's take EM field in a rectangular box with walls that are perfect conductors (optical cavity). EM field distribution inside this cavity can be described with three numbers ## k_x, k_y, k_z ## which when combined give a k-vector: $$ \vec k = k_x \vec e_x + k_y \vec e_y + k_z \vec e_z $$
This ##\vec k## represents one EM mode of oscillation that corresponds to one particular standing EM wave inside this cavity. So far so good.
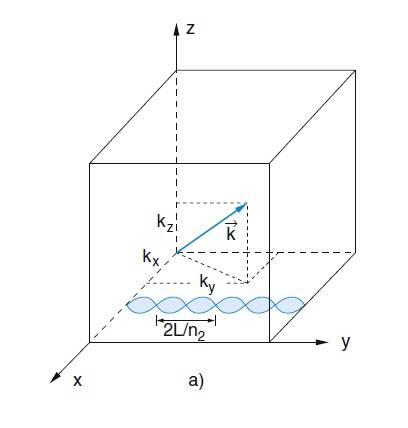
Now, let me take for example z-axis component of this standing wave (or mode) which is represented by ##k_z##. Is it correct to think about this component as the value of electric field in z direction oscillating between some maximum and minimum values eg. in the interval ##[-E_z, +E_z]##? In other words, does ##E_z## oscillates perpendicular to the ##XY## plane?
Same goes for the x and y directions and their components oscilating in ##\vec e_x ## and ## \vec e_y ## directions. When all three combined together ##E_x, E_y, E_z## they would give total electric field for that particular mode.
So far, is this correct visualization that I have in my head?
Now next question, let's take z-axis as the optical axis in which we want to get laser output. Then ## k_x, k_y## would represent transverse modes while ## k_z## would represent longitudinal modes. Is this correct? Now I know that transverse modes will give the laser spot pattern in the output (eg. Gaussian) and that longitudinal modes will give allowed frequencies specific for this particular cavity (resonator) which can be amplified by the gain medium.
Now what I don't understand is how this longitudinal mode fits the picture of laser EM wave (leaving the resonator) which shouldn't have the component in the propagating direction (because EM waves are transverse waves). So if laser ray exits the cavity in z-direction it electric field should lie in the XY plane (eg. have only x and y components and not the z component), correct?
Is it also true then that the seed photon (the one generated by spontaneous emission which starts the laser) must be polarized in such a way that its electric field strictly must have the z-direction in order to hit one of the longitudinal modes?
Let's take EM field in a rectangular box with walls that are perfect conductors (optical cavity). EM field distribution inside this cavity can be described with three numbers ## k_x, k_y, k_z ## which when combined give a k-vector: $$ \vec k = k_x \vec e_x + k_y \vec e_y + k_z \vec e_z $$
This ##\vec k## represents one EM mode of oscillation that corresponds to one particular standing EM wave inside this cavity. So far so good.
Now, let me take for example z-axis component of this standing wave (or mode) which is represented by ##k_z##. Is it correct to think about this component as the value of electric field in z direction oscillating between some maximum and minimum values eg. in the interval ##[-E_z, +E_z]##? In other words, does ##E_z## oscillates perpendicular to the ##XY## plane?
Same goes for the x and y directions and their components oscilating in ##\vec e_x ## and ## \vec e_y ## directions. When all three combined together ##E_x, E_y, E_z## they would give total electric field for that particular mode.
So far, is this correct visualization that I have in my head?
Now next question, let's take z-axis as the optical axis in which we want to get laser output. Then ## k_x, k_y## would represent transverse modes while ## k_z## would represent longitudinal modes. Is this correct? Now I know that transverse modes will give the laser spot pattern in the output (eg. Gaussian) and that longitudinal modes will give allowed frequencies specific for this particular cavity (resonator) which can be amplified by the gain medium.
Now what I don't understand is how this longitudinal mode fits the picture of laser EM wave (leaving the resonator) which shouldn't have the component in the propagating direction (because EM waves are transverse waves). So if laser ray exits the cavity in z-direction it electric field should lie in the XY plane (eg. have only x and y components and not the z component), correct?
Is it also true then that the seed photon (the one generated by spontaneous emission which starts the laser) must be polarized in such a way that its electric field strictly must have the z-direction in order to hit one of the longitudinal modes?