Resultant Moment Couple Problem

[Rico]

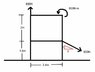
Determine the resultant R and the point on the y-axis through which the line of action of the resultant of the loading system shown passes

I have attached an image of the problem

In my attempt to solve the problem I went about the following steps:
1- I chose my axis to be right in the middle of the 2.4m length along the x axis
2 - Found the x and y components of the resultant force, as well as the magnitude of the resultant and its direction. Rounded off this equaled R = 755.43N and θ = 44.73°
3 - I got lost along this point now: I chose to find out the Resultant x moment and the resultant y moment excluding the moment of 800Nm already given.
4 - I then chose to find resultant moment of the problem by adding the resultant x with the resultant y and then finally adding the 800Nm moment
5 - I then got and answer of - 1340.64... Nm and now I needed to find its position along the y axis, correct? From here I do not know what to do.

Do we make this equation equal to a component of the resultant already worked out or just the resultant. The answer is meant to be 1.31m=y but I can't seem to get this answer.

 

[NascentOxygen]

Hi Rico. http://img96.imageshack.us/img96/5725/red5e5etimes5e5e45e5e25.gif

I'm guessing here, but ... what do you find if you translate the line of action of that 755.43N force so that it produces the -1340Nm moment?

 

[Rico]

Hello NascentOxygen and thank you :)

I consulted several colleagues at my university today and Turns out you do this:

Find the Rx and Ry components of the resultant and then its magnitude. The position of the axis will not affect your final answer. The question asks for the distance along the y-axis for the action of the resultant. This is a distance along +j and needs to be multiplied by a force to equal the sum of all the moments on the object.

So our equation will be:

d-\hat{j} x Rx\hat{i} = ∑M
∴-dR_x=∑M_O^F
∴d=\frac{∑M}{-R_x}

This gives us the distance along the y-axis because it is perpendicular to the Rx component.

Note that ∑M was taken about the lowest left point of the frame. Of course the position of the axis wouldn't actually affect the final result, I just saw it as being the easiest.

My Entire equation was then this (for anyone who is interested)

Angle of force
tanθ=\frac{1}{2}
∴θ=26.565051177° -------> I called this equation A for accuracy

Resultant Force - Components, Magnitude, Direction
R_x = 600cosθ
∴R_x = 536.6563146... N -------> B
∴R_x ≈ 536.66 N

R_x = 800 - 600sinθ
∴R_x = 531.6718427... N -------> C
∴R_x ≈ 531.67 N

|R| = √ R_x² + R_x²
∴|R| = 755.4303067... N
∴|R| ≈ 755.43 N

tanβ = \frac{Ry}{Rx}
∴β = \frac{B}{C}
∴β = 44.73267846... °
∴β ≈ 44.73°

∑M_O^R = M_O^F₁ + M_O^F₂ + M_O^F₃

∴d\hat{j} x R_x\hat{i} = 2.4\hat{i} x 600sinθ-\hat{j} + 1.6\hat{j} x 600cos\hat{i} + 800

∴-dR_x = -2.4(600sinθ) - 1.6(600cosθ) + 800

∴d = \frac{-2.4(600sinθ) - 1.6(600cosθ) + 800}{-600cosθ}

∴d = 1.309288015... m
∴d ≈ 1.31 m

And there it is :) If it had asked for the position along the x-axis then I would've used the R_y component. :)