Review centre of gravity calculation

[PrincessIceFall]

<<Mentor note: Thread merged with duplicate from other forum.>>

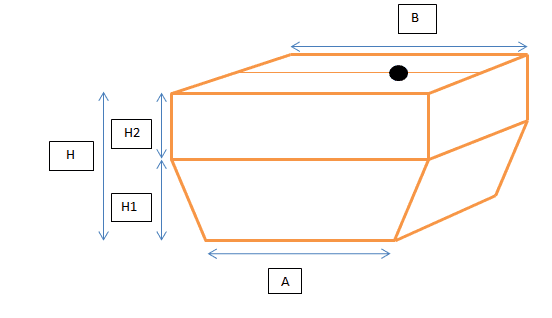
Half an octagonal prism. A small weight is placed 2 cm from the centreline of the vessel. The rod on which the weight is on is placed at (L/2) i.e at the center of the length of the vessel. The height of center of gravity from the base of the vessel is needed to be found.

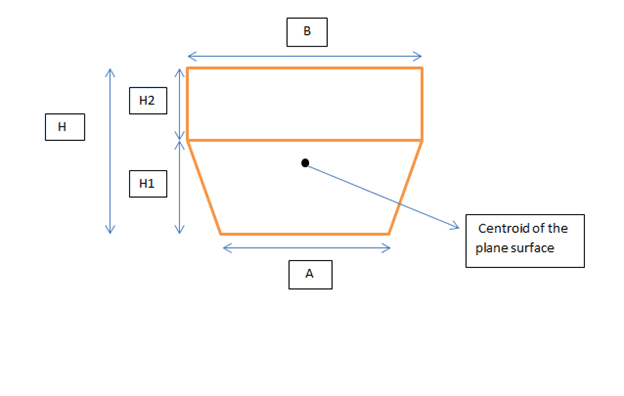
In the above figure

A = 0.12 m

B = 0.2 m

H2 = 0.065 m

H1 = 0.095 m

H = 0.16 m

To find the centroid of the above plane surface, the centroid of each individual shapes must be first found.

The centroid of the trapezium on the x and y-axis from the top is given by the following equations

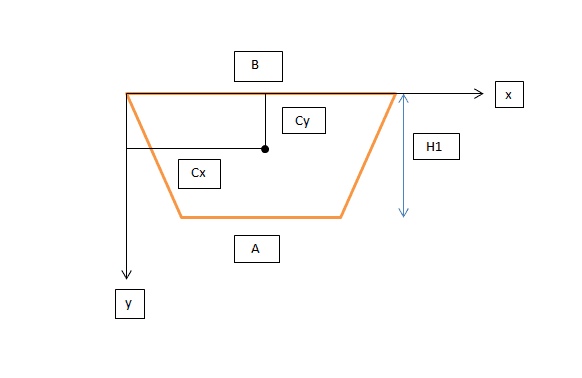
C_x= ( B/2) =0.1 m

C_y= H1/2*[((B+2A)/(B+A))]= 0.095/3*[((0.2+(2*0.12))/(0.2+0.12))]=0.0435 m

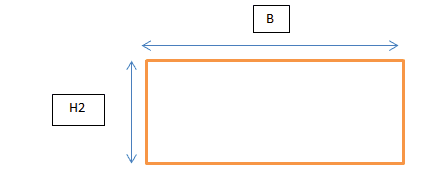
The centroid of the rectangle is simply

C_x= B/2= 0.2/2=0.1 m

C_y= H2/2= 0.065/2=0.0325 m

Now to find the centroid of the whole shape, the following tabular method is used

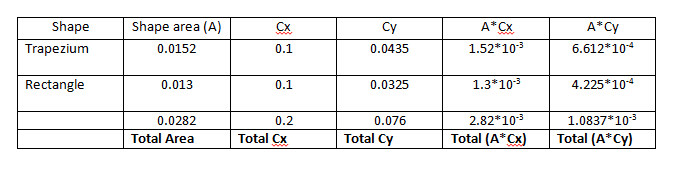
And the centroid of the total area is then given by

C_x= (∑▒〖(A*Cx)〗)/(∑▒A)= (2.82*〖10〗^(-3))/0.0282=0.1 m

C_y= (∑▒〖(A*Cy)〗)/(∑▒A)= (1.0837*〖10〗^(-3))/0.0282=0.03843 m

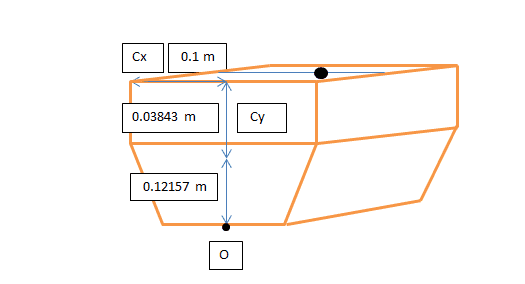
By taking point O as the origin and taking moments around this point w.r.t the y-axis, the height of centre of gravity from the bottom of the keel (base) can be found

W1 = mass of the small weight attached

W = mass of the whole body

KG= ((W1*y1)+(W*y2))/(W1+W)= ((0.05*0.16)+(1.6*0.12157))/(0.05+1.6)=0.1227 m

 

[SteamKing]

I noticed several things in your calculations:

1. The rectangle and the trapezoid are both symmetric with respect to the centerline of the prism. The centroid will therefore lie on the axis of symmetry, i.e., you don't have to calculate this value explicitly.

2. You have measured the vertical center of the rectangle up from its bottom edge, and the vertical center of the trapezoid is measured down from the longer side if the trapezoid. This is incorrect from the standpoint of calculating the vertical moment of the combined trapezoid and rectangle. The location of the center of each figure should be referred to a common location. If you want to use the long side of the trapezoid as your reference, then the centroid location for the trapezoid will be negative, since you are measuring down from the reference, and the centroid of the rectangle will be positive, since you are measuring up from this reference. After calculating the centroid of the entire prism, you must correct this value to the base of the prism if you wish to determine KG.

3. In your tabular form for calculating Cx and Cy, you have shown Total Cx and Total Cy as the sum of the individual Cx and Cy values for the rectangle and the trapezoid. This is incorrect. Total Cx = Total (A * Cx) / Total Area and Total Cy = Total (A * Cy) / Total Area

4. You haven't included the length of the prism or the areas of the sides or bottom in your calculations. The presence of the bottom surface will tend to lower the KG of the prism.

5. It's not clear if the topmost surface of the prism is fully closed, fully open, or something in between. If there is a topmost surface, its presence will tend to raise the KG of the prism.

<<Moderator note: Comments on thread duplication removed.>>

 

[PrincessIceFall]

In your tabular form for calculating Cx and Cy, you have shown Total Cx and Total Cy as the sum of the individual Cx and Cy values for the rectangle and the trapezoid. This is incorrect. Total Cx = Total (A * Cx) / Total Area and Total Cy = Total (A * Cy) / Total Area

That is what I did. Maybe I phrased it wrong, but if you check again, when I calculated Cx and Cy for the total area I used the equation you mentioned.

 

[PrincessIceFall]

It's not clear if the topmost surface of the prism is fully closed, fully open, or something in between. If there is a topmost surface, its presence will tend to raise the KG of the prism.

The topmost surface is hollow.

 

[AlephNumbers]

How did you come up with that equation to express the vertical centroid of the trapezoid? Doesn't the value that you got seem a little suspect?

 

[PrincessIceFall]

The

How did you come up with that equation to express the vertical centroid of the trapezoid? Doesn't the value that you got seem a little suspect?

The equations are from literature.

 

[SteamKing]

That is what I did. Maybe I phrased it wrong, but if you check again, when I calculated Cx and Cy for the total area I used the equation you mentioned.

I did. If you check the table, you'll see that Cx Total is 0.2. But since both the rectangle and the trapezoid have an identical Cx = 0.1, then the Cx Total must also be 0.1.
Perhaps you copied the wrong numbers into the table?

 

[AlephNumbers]

How is it that the centroid is less than half of the value of the height of the trapezoid when more of the mass is concentrated towards the top of said trapezoid?

 

[PrincessIceFall]

You have measured the vertical center of the rectangle up from its bottom edge, and the vertical center of the trapezoid is measured down from the longer side if the trapezoid. This is incorrect from the standpoint of calculating the vertical moment of the combined trapezoid and rectangle. The location of the center of each figure should be referred to a common location. If you want to use the long side of the trapezoid as your reference, then the centroid location for the trapezoid will be negative, since you are measuring down from the reference, and the centroid of the rectangle will be positive, since you are measuring up from this reference. After calculating the centroid of the entire prism, you must correct this value to the base of the prism if you wish to determine KG.

I have measured down from the top for both the reactangle and the trapezium. Why do you feel otherwise?

 

[PrincessIceFall]

You haven't included the length of the prism or the areas of the sides or bottom in your calculations. The presence of the bottom surface will tend to lower the KG of the prism.

How is that so?

 

[SteamKing]

I have measured down from the top for both the reactangle and the trapezium. Why do you feel otherwise?

With the rectangle, you can't be sure where the reference location is, since the c.g. with respect to the top or bottom is the same.

However, the correct calculation for the vertical moment requires that you use the same reference for measuring the height of the c.g. for both the rectangle and the trapezoid. In this case, since you are interested in finding the KG of the prism with respect to the bottom of the prism, then that reference location would be the most logical to choose.

 

[SteamKing]

How is that so?

Think of the KG calculation as finding an average. If we chose the bottom of the prism as the reference location for measuring the height of the c.g. of the various pieces, then the bottom adds area to the calculation but no moment, since it's located at the reference and the c.g. of the bottom is zero. The total moment is still divided by the total area, thus the c.g. must be located closer to the bottom than if only the sides and ends were considered.

It's like trying to find your average grade in a class using the scores on several examinations. If you scored a zero on one of the examinations, this brings your average score down quite a bit.

 

[PrincessIceFall]

Think of the KG calculation as finding an average. If we chose the bottom of the prism as the reference location for measuring the height of the c.g. of the various pieces, then the bottom adds area to the calculation but no moment, since it's located at the reference and the c.g. of the bottom is zero. The total moment is still divided by the total area, thus the c.g. must be located closer to the bottom than if only the sides and ends were considered.

It's like trying to find your average grade in a class using the scores on several examinations. If you scored a zero on one of the examinations, this brings your average score down quite a bit.

But according to theory, if I keep increasing the small weight (say to increments of 50 g) then the KG which is the height of COG from the base will increase. And besides, I am looking at the height which is the y-coordinate, not sure how the length or area comes into play here. And isn't the equation to calculate the COG from point O this:

OG = (m1y1+m2y2)/(m1+m2) ?

Because if that's the equation then why do we need the area?

 

[PrincessIceFall]

With the rectangle, you can't be sure where the reference location is, since the c.g. with respect to the top or bottom is the same.

However, the correct calculation for the vertical moment requires that you use the same reference for measuring the height of the c.g. for both the rectangle and the trapezoid. In this case, since you are interested in finding the KG of the prism with respect to the bottom of the prism, then that reference location would be the most logical to choose.

I get what you are saying. My mistake, I will fix that.

 

[AlephNumbers]

Are you sure that equation is correct though (even if you were to use the same reference)? I calculated the centroid by breaking the trapezoid down into two triangles and a rectangle and I got a significantly different answer. I may very well be making a mistake, however.

 

[PrincessIceFall]

Are you sure that equation is correct though (even if you were to use the same reference)? I calculated the centroid by breaking the trapezoid down into two triangles and a rectangle and I got a significantly different answer. I may very well be making a mistake, however.

I just realized that I have in fact made a mistake. Let me correct it and I will compare my value with yours.

 

[SteamKing]

But according to theory, if I keep increasing the small weight (say to increments of 50 g) then the KG which is the height of COG from the base will increase. And besides, I am looking at the height which is the y-coordinate, not sure how the length or area comes into play here. And isn't the equation to calculate the COG from point O this:

OG = (m1y1+m2y2)/(m1+m2) ?

Because if that's the equation then why do we need the area?

For a body composed of pieces parts made of the same thickness material, the mass of each part will be proportional to the area of the piece.

If you want to compute moments based on the mass of each piece instead of its area, that's acceptable, too.

 

[SteamKing]

But according to theory, if I keep increasing the small weight (say to increments of 50 g) then the KG which is the height of COG from the base will increase. And besides, I am looking at the height which is the y-coordinate, not sure how the length or area comes into play here. And isn't the equation to calculate the COG from point O this:

OG = (m1y1+m2y2)/(m1+m2) ?

Because if that's the equation then why do we need the area?

You should always keep in mind the purpose of calculating the KG of the vessel: you want to confirm the results of your inclining test. When the model vessel is inclined, the KG of the vessel is what determines how much it heels to one side when the test weight is moved. If you want to determine the KG of your model vessel, you can't just assume that the c.o.g. of only the end pieces is the same as the c.o.g. of the entire vessel. Your calculations must include the bottom and sides of the vessel in order to be correct.

 

[PrincessIceFall]

If you want to determine the KG of your model vessel, you can't just assume that the c.o.g. of only the end pieces is the same as the c.o.g. of the entire vessel. Your calculations must include the bottom and sides of the vessel in order to be correct.

In order to do that do I find KG for each of the pieces?

 

[SteamKing]

Are you sure that equation is correct though (even if you were to use the same reference)? I calculated the centroid by breaking the trapezoid down into two triangles and a rectangle and I got a significantly different answer. I may very well be making a mistake, however.

The following link shows the formula for calculating the centroid of a trapezoid knowing the length of the bases and the depth:

http://www.efunda.com/math/areas/isostrapezoid.cfm

 

[SteamKing]

In order to do that do I find KG for each of the pieces?

Yes. Your table needs to expand a bit to add rows for the sides and the bottom, but the principle is the same.

 

[PrincessIceFall]

Yes. Your table needs to expand a bit to add rows for the sides and the bottom, but the principle is the same.

And then what, do I add them all up?

 

[SteamKing]

And then what, do I add them all up?

Yes. Summing the moments and summing the masses works for 2 items or 2000 items.

 

[PrincessIceFall]

Okay let me get this straight. Say that the KG I found for this post, is KG1, now let's multiply that by 2. For the other two sides, its KG2, let's multiply that by 2 too. And for the bottom its KG3. So you are saying that KG for the entire model vessel is:

KG = (KG1*2) + (KG2*2) + (KG3)

 

[PrincessIceFall]

Also, I attaching my KG calculation with this comment. I have made corrections on this one, I used the same reference point. Please verify it for me

 

[SteamKing]

Okay let me get this straight. Say that the KG I found for this post, is KG1, now let's multiply that by 2. For the other two sides, its KG2, let's multiply that by 2 too. And for the bottom its KG3. So you are saying that KG for the entire model vessel is:

KG = (KG1*2) + (KG2*2) + (KG3)

No, you don't find the overall KG by multiplying the individual KG's together with a factor and adding them up.

It's always the same formula: KG_vessel = (KG₁*Mass₁ + KG₂*Mass₂ + ... ) / (Mass₁ + Mass₂ + ...)

where Mass₁, Mass₂, ... , are all the masses of the individual components making up the vessel, and
where KG₁, KG₂, ..., are the KGs of the corresponding individual components making up the vessel

 

[PrincessIceFall]

No, you don't find the overall KG by multiplying the individual KG's together with a factor and adding them up.

It's always the same formula: KG_vessel = (KG₁*Mass₁ + KG₂*Mass₂ + ... ) / (Mass₁ + Mass₂ + ...)

where Mass₁, Mass₂, ... , are all the masses of the individual components making up the vessel, and
where KG₁, KG₂, ..., are the KGs of the corresponding individual components making up the vessel

There is no way for me to know the mass of each of the parts. I only know the mass of the whole vessel. What do you suggest I do then?

 

[SteamKing]

There is no way for me to know the mass of each of the parts. I only know the mass of the whole vessel. What do you suggest I do then?

That was the whole point of the exercise.

By breaking down the hull of the vessel into simple geometrical shapes, like rectangles and trapezoids, the mass of each piece could be estimated and its individual KG calculated. Once all of this information had been compiled, then an estimate of the total mass of the vessel and its KG could then be made, to compare with the data obtained from the inclining experiment.

Granted, you are doing this experiment on a vessel with a simple hull, but this should allow you to make a reasonable attempt at doing an accurate calculation. You had made a start by doing the calculations for the ends of the vessel. I don't see why including the sides and bottom should be any more difficult than what you have already done.

Is this vessel somehow more complicated in construction than discussed?

 

[PrincessIceFall]

That was the whole point of the exercise.

By breaking down the hull of the vessel into simple geometrical shapes, like rectangles and trapezoids, the mass of each piece could be estimated and its individual KG calculated. Once all of this information had been compiled, then an estimate of the total mass of the vessel and its KG could then be made, to compare with the data obtained from the inclining experiment.

Granted, you are doing this experiment on a vessel with a simple hull, but this should allow you to make a reasonable attempt at doing an accurate calculation. You had made a start by doing the calculations for the ends of the vessel. I don't see why including the sides and bottom should be any more difficult than what you have already done.

Is this vessel somehow more complicated in construction than discussed?

Okay, I am not sure you understand how I calculated KG for this post. I did not take mass of that specific end, I took the mass of the whole vessel (which was 1.6 kg) and assumed it to be concentrated in the center and then multiplied this mass with the distance of the center from the base.

 

[PrincessIceFall]

Here are pictures of what the vessel actually looks like.