Why Is My Rigid Body Equilibrium Equation Incorrect?

[dbag123]

Homework Statement

Determine the lenght of h with respect to b so that the water flows.

Relevant Equations

sum of moments at the hinge

Hello

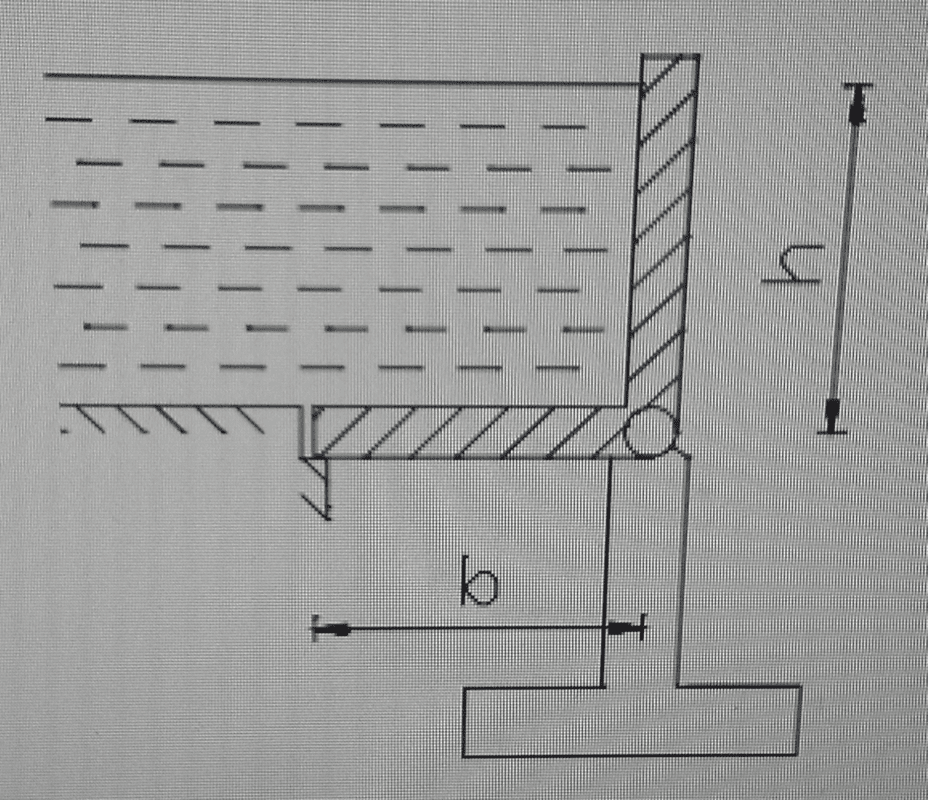
Ihave gotten as far as coming up with an equation for the sum of moments and it goes as follows: bh*1/2b-1/2hb*1/3b=0 the answer for h i get is wrong and i don't know if i am missing something. moment arm on the b is 1/2b and the moment arm on h is 1/3h because of the way water pressure works , meaning its a uniform load in the shape of triangle. bh is my way of writing the force as a point load acting on the levers. The answer to this problem is supposed to be h= √3 *b. Any help is appreciated.

 

[jbriggs444]

sum of moments and it goes as follows: bh*1/2b-1/2hb*1/3b=0

In your expression for the torque on the vertical wall, why does b enter in?

 

[dbag123]

In your expression for the torque on the vertical wall, why does b enter in?

my thinking was that replacing the acting force with the area of water would be of help, but yeah its not helping

 

[jbriggs444]

my thinking was that replacing the acting force with the area of water would be of help, but yeah its not helping

I do not think that you are catching on. The wall is h meters high, not b meters high.

 

[dbag123]

I do not think that you are catching on. The wall is h meters high, not b meters high.

My thinking was that the resultant force acting on the vertical Wall would be 1/2hb(area of triangle) and the moment arm 1/3h from the hinge and the product of these 2 then the moment​

 

[jbriggs444]

My thinking was that the resultant force acting on the vertical Wall would be 1/2hb(area of triangle) and the moment arm 1/3h from the hinge and the product of these 2 then the moment

The average pressure on the wall is proportional to the height of the wall. The higher the wall, the higher the average pressure.

The total force on the wall is proportional to the height of the wall [times the average pressure]. The higher the wall, the higher the total force.

The total torque on the wall is proportional to the height of the wall [times the total force]. The higher the wall, the higher the total torque.

The length of the floor segment does not enter into the calculation of torque on the vertical wall. You can use a triangle to calculate the force on the vertical wall. Just not the particular triangle you have in mind.

 

[dbag123]

The average pressure on the wall is proportional to the height of the wall. The higher the wall, the higher the average pressure.

The total force on the wall is proportional to the height of the wall [times the average pressure]. The higher the wall, the higher the total force.

The total torque on the wall is proportional to the height of the wall [times the total force]. The higher the wall, the higher the total torque.

The length of the floor segment does not enter into the calculation of torque on the vertical wall. You can use a triangle to calculate the force on the vertical wall. Just not the particular triangle you have in mind.

And that's why my moment equation does not work. Thank you.