Roller coaster and centripetal acceleration

[annamal]

Homework Statement

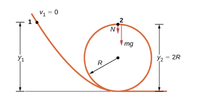
The frictionless track for a toy car includes a loop-the-loop of radius R. How high, measured from the bottom of the loop, must the car be placed to start from rest on the approaching section of track and go all the way around the loop?

Relevant Equations

Fc = m*v^2/r
-m*g(y2 - y1) = 0.5*m*v2^2

See attached image.
The solution to this problem calculates v2 at the top of the roller coaster ride. Why is that? Shouldn't you calculate v2 at the bottom of the roller coaster ride as you require the maximum velocity there to get around the loop?

 

[haruspex]

The solution to this problem calculates v2 at the top of the roller coaster ride. Why is that? Shouldn't you calculate v2 at the bottom of the roller coaster ride as you require the maximum velocity there to get around the loop?

And what does it do with the velocity it calculated?

 

[annamal]

And what does it do with the velocity it calculated?

That's just the velocity going around the roller coaster.

 

[haruspex]

That's just the velocity going around the roller coaster.

That does not answer my question. What equations does the solution have which involve v2?

 

[Orodruin]

That's just the velocity going around the roller coaster.

Velocity on the roller coaster is not the relevant question (and is also not constant in the loop for obvious reasons). The relevant question is: When and why would the car risk falling off the roller coaster?

 

[Lnewqban]

...
The solution to this problem calculates v2 at the top of the roller coaster ride. Why is that? Shouldn't you calculate v2 at the bottom of the roller coaster ride as you require the maximum velocity there to get around the loop?

If the toy is properly designed, placing the car at the top end of the ramp will be sufficient.
Now, imagine that you are the designer of the toy and that the only information given to you are the diameter of the loop and the requirement to save material and package volume by making the ramp as short as possible.
Bonus question: Could you manipulate the weight of the car to reduce the ramp height?

 

[annamal]

That does not answer my question. What equations does the solution have which involve v2?

Fc = m*v^2/r
-m*g(y2 - y1) = 0.5*m*v2^2

 

[annamal]

And the incline to the loop at the beginning is negligible why?

 

[Lnewqban]

And the incline to the loop at the beginning is negligible why?

Apply what you have learned about pure potential and pure kinetic energy, as well as about a mix of both.

 

[haruspex]

Fc = m*v^2/r
-m*g(y2 - y1) = 0.5*m*v2^2

Still something missing.
The first of those two is the general expression for centripetal force. It does not mention v2 as such. Isn't there another equation using v2 instead of the generic v?